公務員試験 2020年 国家一般職(土木) No.26解説

　問 題　　　　　

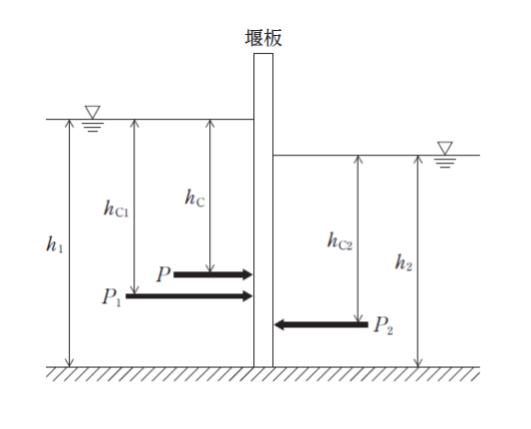
図のように、幅 (奥行き方向) が単位幅の鉛直な堰板で水域を仕切っている。堰板の左側に作用する全静水圧を P₁、作用点の水深を h_C1、堰板の右側に作用する全静水圧を P₂、作用点の水深を h_C2 とすると、この堰板に作用する全静水圧の合力 P、作用点の水深 h_C の組合せとして最も妥当なのはどれか。

ただし、水の密度を ρ、重力加速度の大きさを g とし、P は右向きを正とする。

 

 

 

 

 

　解 説　　　　　

【静水圧の基礎知識】
静水圧のポイントは以下２つです。

・水圧は面に垂直に働きます。
・水圧は深くなるほど大きくなります。※ 高さ H の時、水圧は ρgH です。

全水圧は水圧の三角形分布を図示した際の、三角形の面積です。最も深い部分の水圧：ρg H が底辺、高さを H より、全水圧 = ρgH²/2 です。

【全静水圧の合力 P】
堰板左側に注目すれば、全水圧は ρgh₁²/2…(1) です。
堰板右側に注目すれば、全水圧は ρgh₂²/2…(2) です。

従って
堰板に作用する全静水圧の合力 P = (1) – (2)
= ρg(h₁² – h₂²)/2 となります。正解は 1 or 2 です。

【作用点の水深 h_c】
・モーメントの和が 0 なので
P × h_c + P₁ × h_c1 = -P₂ × {(h₁ – h₂) + h_c2} です。
※ P、P₁　と P₂ は向きが逆なので、符号が逆です。

h_c = {P₁h_c1 – P₂((h₁ – h₂) + h_c2)}/P です。

以上より、正解は 2 です。

類題 H26 no27
https://yaku-tik.com/koumuin/h26-doboku-27/