問 題
待ち行列モデルに関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。
「あるネットワークプリンタでは、 1 分当たり平均 2 件のジョブを受信し、ジョブ 1 件当たり平均 15 秒の処理時間を要する。このネットワークプリンタにおけるジョブの受信及びその処理が M/M/1 待ち行列モデルに従うものとするとき、利用率 ρ は ㋐ と求まる。
この ρ と、処理中及び処理待ちを合わせた待ち行列の平均の長さ(平均滞留件数)L の間に、L = ρ/(1 – ρ)の関係があることを用いると、ジョブの受信から処理開始までの平均待ち時間は ㋑、ジョブの受信から処理終了までの平均応答時間は ㋒ とそれぞれ求まる。」
解 説
【待ち行列について】
待ち行列は、人や物がサービスを待つ列(待ち行列)についてのモデルです。窓口が 1 つの M/M/1 モデルが代表例です。◯/△/▢ という表記はケンドールの記号 と呼ばれる表記法です。先頭から「到着の過程」、「サービス提供時間の分布」、「サービスの数」を表しています。イメージが以下の通りです。
M/M/1 モデルにおいて、単位時間当たりの 平均到着数を λ(/分)、単位時間当たりの平均処理数を μ(/分)とすると、平均利用率 ρ は ρ = λ/μ と表されます。
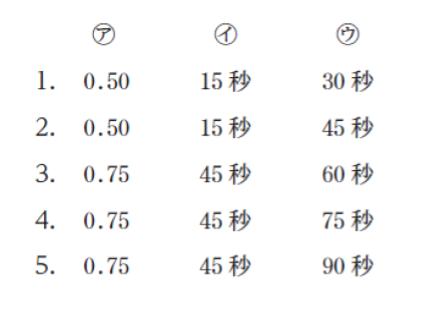
本問では、「ジョブを 1 分あたり 2 件受診」なので、「客」に対応するものが 「1 分あたり 2」やってきます。「平均到着数 λ = 2」です。そして、15 秒で ジョブ 1 件処理なので、1 分あれば 4 件処理できます。「平均処理数 μ = 4」です。従って、利用率 t = 2/4 = 0.50 です。 ㋐ は 0.50 です。正解は 1 or 2 です。これにより、㋑ は 15 秒とわかります。
㋒ ですが
ジョブの受信から処理終了は 受信 → 処理開始までの待ち時間 → 処理時間 と分解できます。㋑ より「受信から処理開始までの平均待ち時間」が 15 秒なので、後はジョブ処理時間を足せば ㋒ がわかります。1件のジョブは 平均 15 秒で処理できるので 15 + 15 = 30 秒です。
以上より、正解は 1 です。
類題 H30no36 待ち行列
https://yaku-tik.com/koumuin/h30-denjyou-36/

コメント