問 題
次の連立不等式の解として正しいのはどれか。
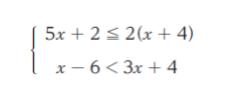
1.x < -5
2.-5 < x ≦ 2
3.-4 < x ≦ 2
4.x ≦ 2
5.x ≧ 5
正解 (2)
解 説
解法1:各不等式を解く
上:5x + 2 ≦ 2x + 8 ⇔ 3x ≦ 6 ⇔ x ≦ 2
下:-2x < 10 ∴ x > -5 です。
連立不等式の解は -5 < x ≦ 2 とわかります。
以上より、正解は 2 です。
解法2:選択肢に注目し、適当な値を代入することで不等式が成立するか評価する。(公務員試験全般に通じる点から、おすすめ)。
選択肢 に注目すると
各選択肢は数直線上に、以下のように図示できます。
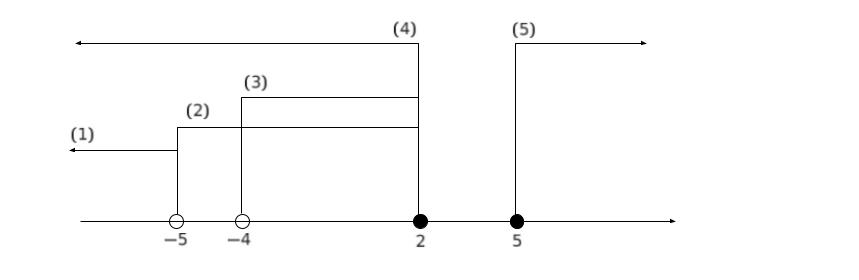
x として、極端に大きな数や小さな数から検討します。
一例として、 x = -10, x = 10 の場合について、各不等式に代入して評価します。
【x = -10 の場合】
上式 左辺 ー48。上式 右辺 ー12。 右辺の値の方が大きいため、OK。
下式 左辺 ー16。下式 右辺 ー26。 右辺の値の方が小さく、成立していない。ダメ。
これにより、x = ー10は連立不等式の解ではないとわかります。そのため、x = ー10が入ってしまうような、(1),(4) は誤りです。
同様に x = 10 の場合を評価すると
上式が成立せずダメです。そのため、x = 10 が入ってしまう (5) は誤りです。
(2),(3) のどちらであるかを判断するためには、ー5 ~ ー4の部分の適当な値で評価すればよいです。そこで、x = ー 4.5 の場合を考えてみます。すると、上式も下式も成立します。ぜひ自分で確認してみてください。従って、正解は -5 < x ≦ 2 です。
以上より、正解は 2 です。

コメント