問 題
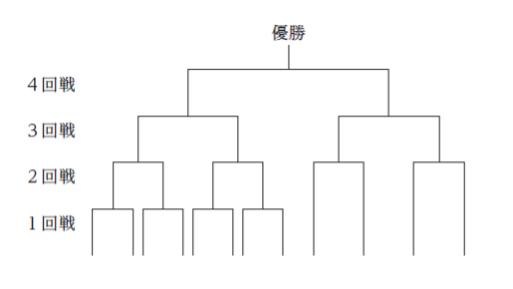
ある町で,12 チームが参加するバレーボールの大会がトーナメント方式で行われることとなり,図のような, 8チームが1回戦から参加し, 4 チームが2回戦から参加するトーナメント表を作成した。
しかし,参加するチームが 1 チーム増えて 13 チームになったことから,トーナメント表を修正し, 1 回戦から参加するチームを 8 チームから 10 チームに, 2 回戦から参加するチームを 4 チームから 3 チームに変更することとした。次の大会開催規則に従って試合をする場合,確実にいえるのはどれか。ただし,全ての試合において勝敗が必ず決まるものとする。
[大会開催規則]
○ 1 日に行うことができるのは 3 試合までである。
○ 同じチームが 1 日に 2 度試合することはない。
1.参加するチームが 1 チーム増えたことで,この大会の総試合数は 2 試合増えることになった。
2.各チームにとっての 1 試合目で敗退するチーム数と, 2 試合目で敗退するチーム数の比は,2 : 1 である。
3.各チームにとっての 1 試合目と 2 試合目の間が最も長いチームは, 1 試合目後の 3 日間は試合がない。
4. 3 試合に勝利したチームは準優勝チームになる。
5.優勝チームが決まるまでにかかる最短の日数は 5 日である。
解 説
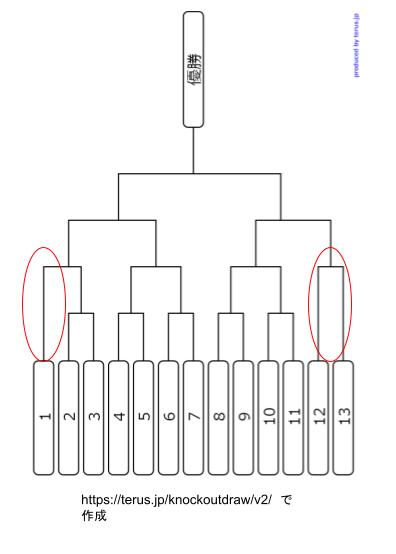
1例として、以下のようにトーナメント表が変更されたと考えます。(変更部分は赤丸部分)。
選択肢 1 ですが
変更前と、変更後のトーナメント表の試合数を数えれば、もともと11試合が、12試合になっています。2試合ではなく、1試合増えています。選択肢 1 は誤りです。
選択肢 2 ですが
チーム2~チーム13までの試合に注目すると、第1試合で6チーム敗退します。そして、左赤丸で囲った「1」のチームがもし初戦で負けると、第1試合で7チーム敗退することになり、2試合目で敗退するチーム数が何であれ、2:1にはなりません。選択肢 2 は誤りです。
選択肢 3 ですが
チーム2-3での試合でチーム2が勝ったとします。
以下
1日目:2-3、4-5、6-7 の3試合
2日目:8-9、10-11 ここまでで1回戦終了なので、以下、2回戦を消化していくとします。
すると、(1回戦で勝った)チーム2の2回戦を一番遅くしたとしても、3日目で試合を回すことができます。このパターンにおいて、1試合目と2試合目の間が最も長いのは、チーム2です。そして、1試合目後の2日間しか、試合がない日はありません。従って、「1 試合目後の 3 日間は試合がない」と確実にはいえません。選択肢 3 は誤りです。
選択肢 4 ですが
変更後のトーナメント表を見ると、チーム1,12,13は3試合勝利すると優勝です。選択肢 4 は誤りです。
1~4が誤りなので、正解は 5 です。

コメント