問 題
A,B,C の 3 人が徒競走を 4 回行った。徒競走を 1 回行うごとに, 1 位になった人は,他の 2 人から 1 位になった人が持っているのと同じ枚数のメダルをそれぞれ受け取る約束をした。次のことが分かっているとき,初めにBが持っていたメダルは何枚か。ただし,同着はなかったものとする。また, 1 位になった人は常に約束どおりの枚数のメダルを受け取ったものとする。
○ 1 回目の徒競走では,Bが1 位になった。
○ 2 回目と3 回目の徒競走では,Aが1 位になった。
○ 4 回目の徒競走では,Cが1 位になり,AとBからそれぞれ 27 枚のメダルを受け取った。その結果,AとBのメダルはちょうどなくなった。
1. 11 枚
2. 13 枚
3. 15 枚
4. 17 枚
5. 19 枚
解 説
1位の人のメダルが 3倍になるゲームです。初期状態の A,B,C のメダルを A0、B0、C0 とします。
1回目の徒競走の結果、B のメダルは3倍になり、A,C のメダルは B0 だけ減ります。まとめると、以下のようにメダルの所持数が推移します。
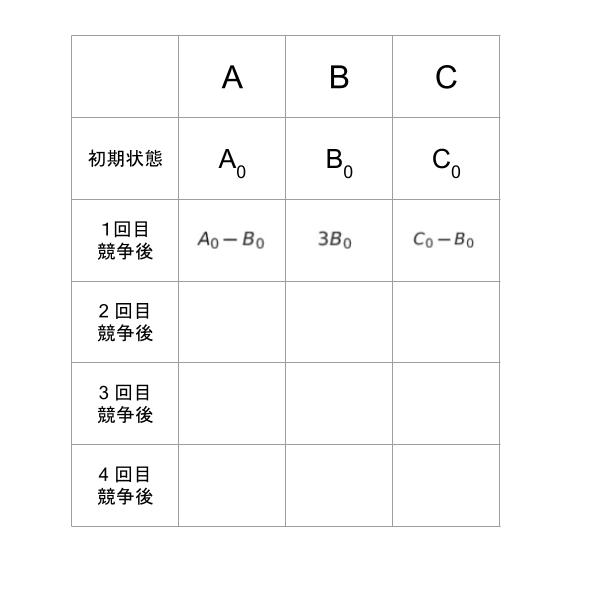
2,3回目で A が 1 位になることから、A のメダルは、1回目終了後から見て9倍になります。そして、次の4回目で C が1位になり、A が 27 枚メダルを C にわたしてちょうどなくなることから、3回目の徒競走が終わった時点で A は 27 枚メダルを有しています。逆に考えれば、1回目の徒競走が終わった時点での A のメダルは 27 ÷ 9 = 3 枚とわかります。ここまでを表にしてみると、以下のようになります。
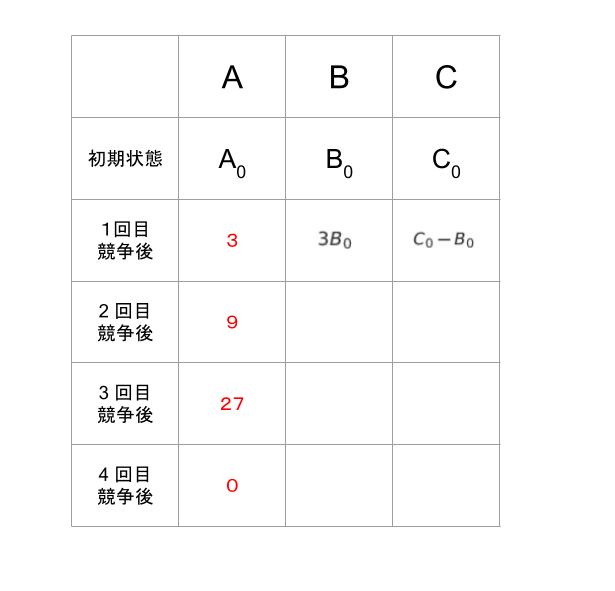
A の列が具体的数で埋まったため、2回目競争後の B は 3B0 ー3、3回目競争後の B は 3B0 ー 12 と表すことができます。
3回目競争後時点で B は、A と同じく 27 枚有していなければなりません。つまり、3B0 ー 12 = 27 です。従って、B0 = 13 とわかりました。
以上より、正解は 2 です。

コメント