問 題
効用を最大化する,ある個人の効用関数が以下のように示される。
u = x(24 – L)
(u:効用水準,x:X財の消費量,L:労働時間 (単位:時間, 0 < L < 24))
この個人は,労働を供給して得た賃金所得と非労働所得の全てをX財の購入に充てるものとし,1 日(24 時間)を労働時間か余暇時間のいずれかに充てるものとする。
X財の価格を 2 ,非労働所得を 60 とするとき,この個人の労働供給関数として妥当なのはどれか。ただし,w(w > 0)は時間当たりの賃金である。
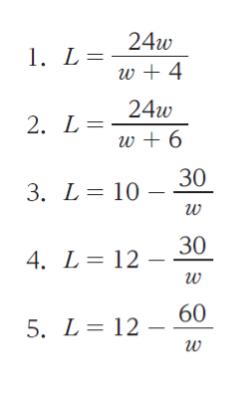
正解 (4)
解 説
具体的な数で、問題を自分なりに把握すると見通しが立てやすいかと思います。一例として、w = 6 と勝手に設定してみます。すると、L 働けば、6L の賃金所得を得ます。非労働所得が 60 なので、全所得は 6L + 60 となります。
X 財の価格が 2 なので、X 財の消費量は (6L+60) ÷ 2 = 3L + 30 です。従って、u = (3L + 30)(24 – L) と表されます。展開すると、u = -3L2 + 42L + 720 です。微分すれば u’ = -6L + 42 です。効用最大の時、u’ = 0 です。従って、効用最大の時、労働時間 L = 7 です。w を具体的に設定してみた所、効用最大化される L が具体的に求まりました。
選択肢 を見ると、すべて w が決まれば L がわかる関係式 になっています。そして、w = 6 を代入してみると、L = 7 となるのは、L = 12 – 30/w という式のみです。従って、この式が正しいと考えられます。
以上より、正解は 4 です。

コメント