公務員試験 2019年 国家一般職(高卒 技術) No.66解説

　問 題　　　　　

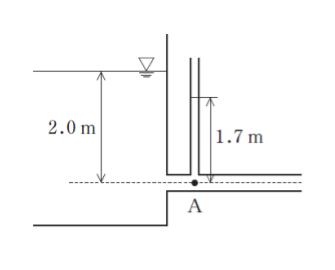
図のように，水槽の水面から深さ 2.0 m の位置に中心がくるように取り付けた，断面積が 5.0 × 10² mm² の一様な円管に流量 1.0 × 10^-3 m³/s の水を流したところ，円管の入り口近くの点 A に設けたマノメータの水位が 1.7 m であった。このとき，流入損失係数はおよそいくらか。

ただし，水槽の水深は変化せず，水槽と円管の急縮部分以外でエネルギー損失はないものとする。また，重力加速度の大きさを 10 m/s² とする。

1． 0.40
2． 0.50
3． 0.60
4． 0.70
5． 0.80

 

 

 

 

 

　解 説　　　　　

急縮前後における 損失水頭を Δh、流入損失係数を f とおきます。
Δh = f・v²/2g ・・・（１）が成立します。これは基礎知識です。

 

Δｈ を求めるために
まず、連続の式（Q = Av）より、A 点における流速を求めます。
mm² = 1.0 × 10^-6 m² と、単位を合わせてから公式に数値を代入すると
1.0 × 10^-3 = 5.0 × 10^-4 × v 　です。

∴ A 点における 流速 v = 2.0 m/s です。

A 点における圧力水頭が 1.7m
A 点における速度水頭が v²/2g = 4/20 = 0.2 です。合計 1.9 です。

一方、急縮直前において
水頭は 2.0m です。差である Δh は 2.0 ー 1.9 = 0.1 です。これで、流入損失係数 f を求める準備ができました。

 

（１）より
0.1 = f・2.0²/(2 × 10) が成立します。
∴ f = 0.50 です。

 

以上より、正解は 2 です。