問 題
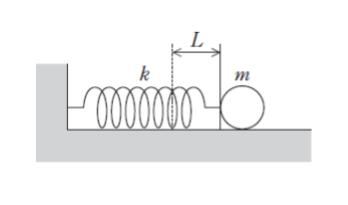
図のように,滑らかな水平面上に置かれた質量 m の小球にばね定数 k の軽いばねを取り付け,他端を壁に固定した。いま,小球を引っ張って,ばねが自然長から L 伸びた水平面上の点まで移動させ,小球を静かに放した。このとき,ばねの長さが自然長になる点での小球の速さとして最も妥当なのはどれか。
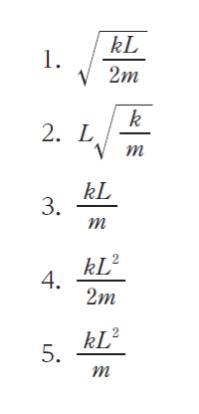
正解 (2)
解 説
水平ばね振り子において
弾性力による位置エネルギー U は、基準点(自然長)から x 離れた所において
U = kx2/2 です。これは知識です。
また、力学的エネルギー = 位置エネルギー+運動エネルギー が、どの位置においても同じ値をとります。運動エネルギー K = mv2/2 です。
【ばねが自然長から L 伸びている状態】
自然長から L 伸びているので、位置エネルギーが kL2/2、動いていないので、運動エネルギー 0 です。従って、力学的エネルギー:kx2/2 + 0 = kL2/2 ・・・(1)です。
【ばねの長さが自然長になる点】
位置エネルギーが 0 です。この時の小球の速さを v とおけば、運動エネルギーが mv2/2 です。従って、力学的エネルギー:0+ mv2/2 = mv2/2 ・・・(2)です。
力学的エネルギーが保存されるため、(1)=(2)です。
v について解くと、以下のようになります。

以上より、正解は 2 です。
類題 H29no15

コメント