公務員試験 2019年 国家一般職(高卒 技術) No.8解説

　問 題　　　　　

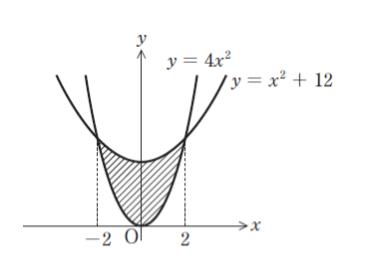
図のように，xy 平面上において曲線 y = x²+ 12 と曲線 y = 4x² で囲まれた領域の面積はいくらか。

1．　8
2． 16
3． 24
4． 32
5． 40

 

 

 

 

 

　解 説　　　　　

解法１【面積の概算】

与えられた図は、少し縦横の縮尺が、おそらく印刷の都合上修正されています。できるだけ手元で正確な図を書いてみると、以下のような細長いグラフとなることがわかります。

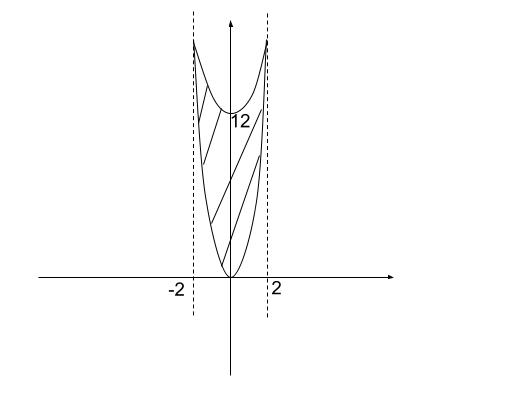
斜線部の大体の面積を求めます。下図のように注目します。

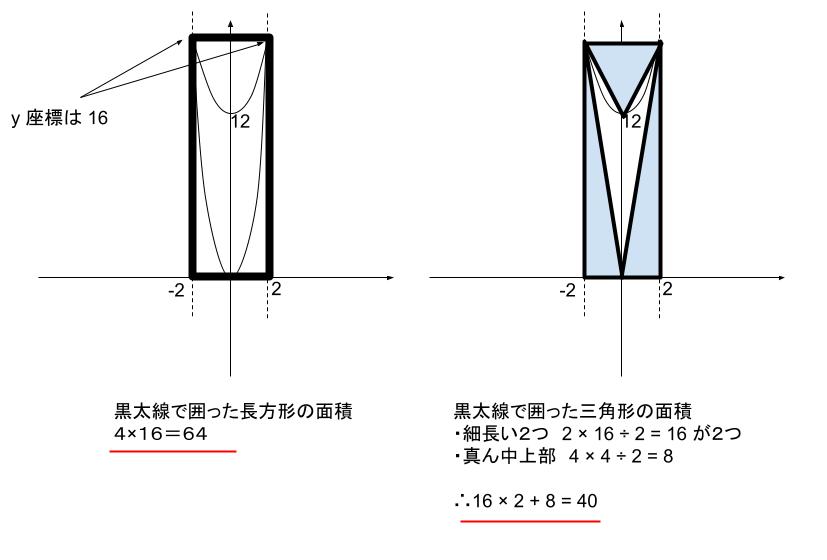
６４－４０＝２４が大体の斜線部の面積と概算できます。

そして
細長い三角形が斜線部を相当えぐっているように見えるため、斜線部は２４より少し大きいと考えられます。そのため、２４より大きいもので、２４に近いものを選べば、正解は 4 です。

解法２【定積分による面積計算】

斜線部は x = -2 ~ 2 において、上端は y = x² + 12 、下端は y = 4x² に挟まれた部分です。このような部分の面積は  ∫ （上端の式ー下端の式）の 定積分で計算することができます。

まず、不定積分をすると、以下のようになります。

不定積分で求めた式に対して
「上に書かれた小さな数値を代入した値ー下に書かれた小さな数値を代入した値」　が　定積分です。

x = 2 を代入すると 16、x = -2 を代入すると ー16 なので、定積分の結果 32 という値が出てきます。以下のようになります。

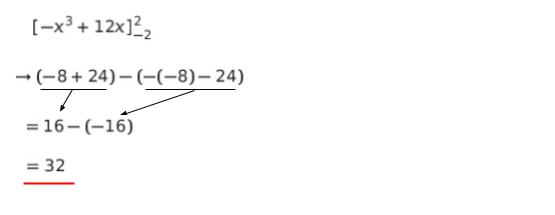
以上より、正解は 4 です。
類題 H30 no7