公務員試験 2019年国家一般職(土木) No.21解説

　問題　　　　　

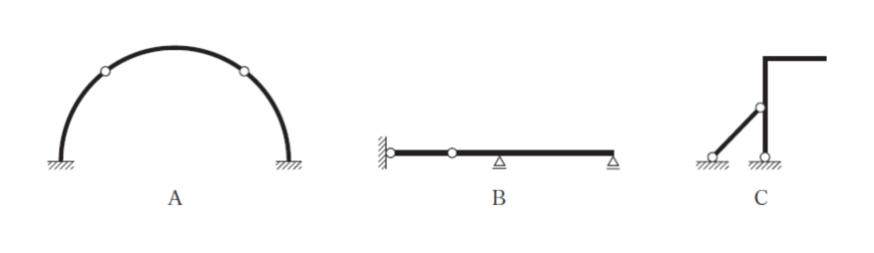
図のような構造物 A、B、C のうち静定構造物のみを全て挙げているのはどれか。

1．A
2．A、B
3．A、C
4．B
5．B、C

正解 (5)

　解説　　　　　

静定構造物であれば n + s + r – 2k = 0…(1) が成り立ちます。

n = 反力数
s = 部材数=支点 or 節点（ー◯ー）で区切られた区間
r = 剛接接合材数：ばきっと折れてる部分で区切る
k = 節点数（支点含む）　です。

A ですが
固定支点なので、1 つの固定支点ごとに反力が 3 あります。従って、n = 3 × 2 = 6 です。部材数は 3 です。r = 0 です。k = 4 です。

(1) の右辺を計算すれば 6 + 3 + 0 – 2 × 4 = 1 ≠ 0 です。静定構造物ではありません。これにより、正解は 4 or 5 です。また、B は静定構造物とわかります。

C ですが
ピン支点なので、1 つの支点ごとに反力が 2 あります。n = 2 × 2 = 4 です。部材数は 3 です。 r = 1 です。k = 4 です。

(1) の右辺を計算すれば 4 + 3 + 1 – 2 × 4 = 0 です。静定構造物とわかります。

以上より、正解は 5 です。

コメント