問 題
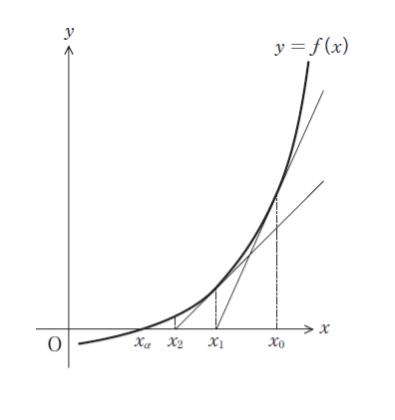
図のような関数 f(x) について、ニュートン法により、f(x) = 0 のある解 xa の近似値を求める。まず、xa に近いと考えられる初期値 x0 を選び、点 (x0、f(x0)) における y = f(x) の接線を引くと、この接線が x 軸と交わる点 x1 は、x0 よりも xa に近づく。これを繰り返すことにより、xa の近似値を求めることができる。
このとき、k + 1 番目の近似値 xk+1 を k 番目の近似値 xk で表したものとして最も妥当なのはどれか。
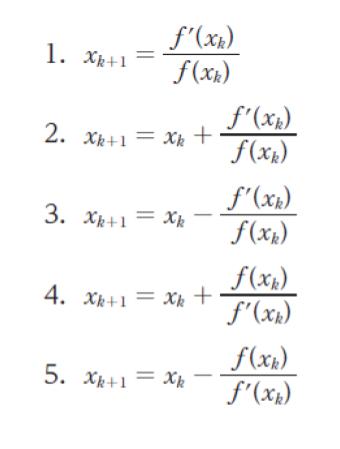
正解 (5)
解 説
k = 0 の場合を考えます。
初期値 (x0、f(x0)) から接線を引いて、x 軸と交わった所の x 座標が x1 です。まず、接線の式を求めると y = f'(x0)x -f'(x0)x0 + f(x0) です。計算過程は以下のようになります。
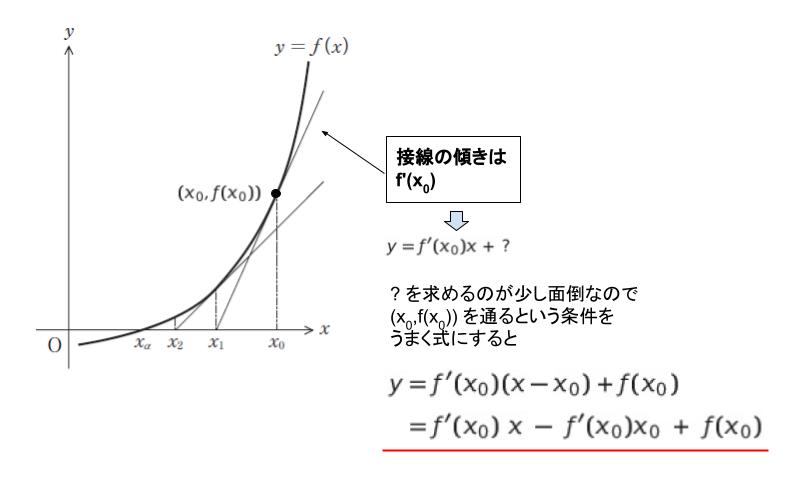
接線の式に、y = 0 を代入して、x = … となおせば、その時の x 座標が x1 です。
従って
x1 = {f'(x0)x0 – f(x0)}/f'(x0)
= x0 – f(x0)/f'(x0) です。
k = 0 を選択肢に代入すれば、同じ形になるのは
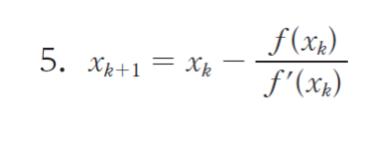
以上より、正解は 5 です。
類題 H25no35 ニュートン法
https://yaku-tik.com/koumuin/h25-denjyou-35/

コメント