2019年 国家一般職(電気・電子・情報) No.24解説

　問 題　　　　　

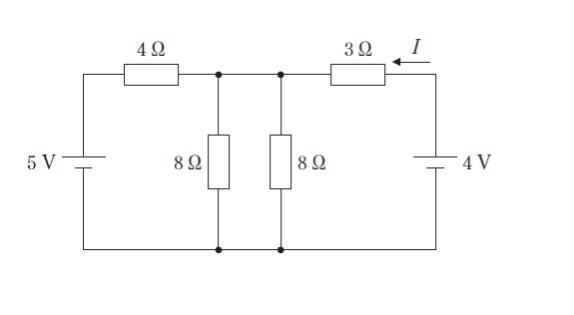
図のような回路において、電流 I の大きさはおよそいくらか。

1．0.1 A
2．0.2 A
3．0.3 A
4．0.4 A
5．0.5 A

 

 

 

 

 

　解 説　　　　　

電池が 2 つ以上あるので、キルヒホッフの法則を思い出します。電流の枝分かれがいくつかあるため、一例として I₁,I₂ とおいて、電流則より各部分の電流を、以下のように表します。向きなどについて、各自のやり方でかまいません。

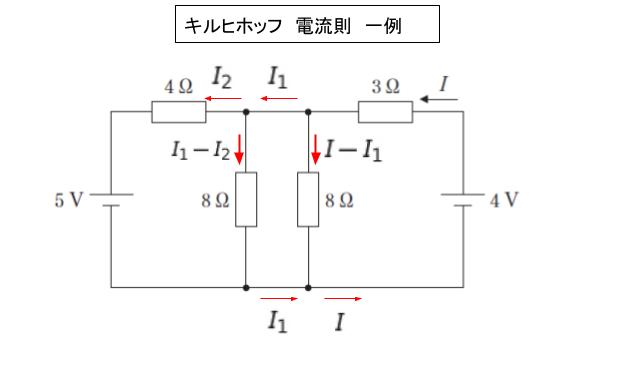
次に電圧則より、例えば以下のように 3 つの閉回路に注目します。これも各自のやり方でかまいません。

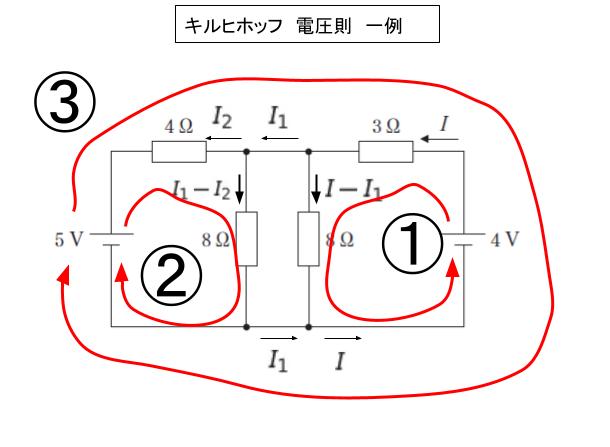
① の閉回路で『起電力の和 = 電圧降下 の和』より
4 = 3 I + 8(I – I₁) です。整理して 4 = 11I – 8I₁ ・・・(1)

②  の閉回路で『起電力の和 = 電圧降下 の和』より
5 = 4 × (-I₂) + 8(I₁ – I₂) です。注目する閉回路と 仮定した電流の向きが逆なので「-I₂」である点に注意が必要です。整理すれば、5 = 8I₁ – 12I₂ ・・・(2)

③  の閉回路で『起電力の和 = 電圧降下 の和』より
5 – 4 = 4 × (-I₂) + 3 × (-I) です。整理して 1 = -4I₂ -3I ・・・(3)

未知数 3 つ (I,I₁,I₂) で式 3 つなので解けると判断して、I を求めます。解き方の一例が以下のようになります。I が出ればどうやっても OK です。

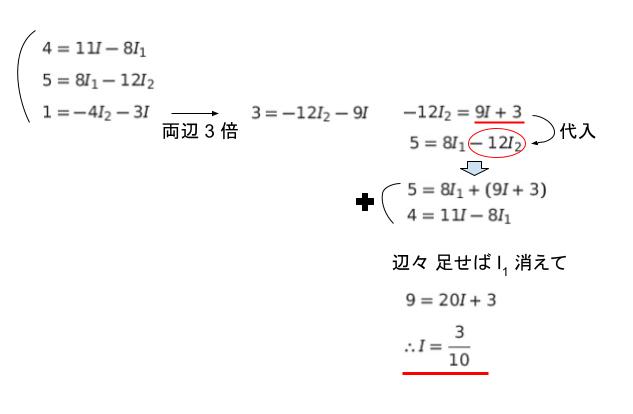
以上より、正解は 3 です。

類題 国家一般職　高卒技術　2021 no21 
https://yaku-tik.com/koumuin/2021-gijyutu-21/