R2年 汚水処理特論 問3 問題と解説

　問 題　　　　　

排水中の懸濁粒子を沈降分離で処理する場合、一般に、懸濁粒子は下記のストークスの式に従って沈降する。直径d=0.01cm、密度ρ_s=1.2g/cm³の懸濁粒子の最も近い沈降速度v(cm/s)はいくらか。

ただし、懸濁粒子は球形で、沈降過程における凝集はなく、沈殿池内に乱れや短絡流はないものとする。

ここに、

• v：粒子の沈降速度 (cm/s)
• g：重力の加速度 = 980 cm/s²
• d：粒子の直径 (cm)
• μ：水の粘度 = 0.01 g・cm^-1・s^-1
• ρ_s：粒子の密度 (g/cm³)
• ρ：水の密度 = 1.0 g/cm³

1. 0.054
2. 0.11
3. 0.54
4. 1.1
5. 5.4

 

 

 

 

 

　解 説　　　　

ストークスの式は最重要公式なので、計算式とそれぞれの変数が何を指すのかを、しっかりと覚えておいてください。今回は問題文に式が与えられていますが、この式が載っていない出題パターンも多く、知識として知っておかないと正解できない場合もあります。

今回は式が与えられているので、問題文に記載された各数値を代入して計算すれば正解が得られます。

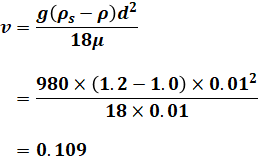
以上から、正解は(2)です。