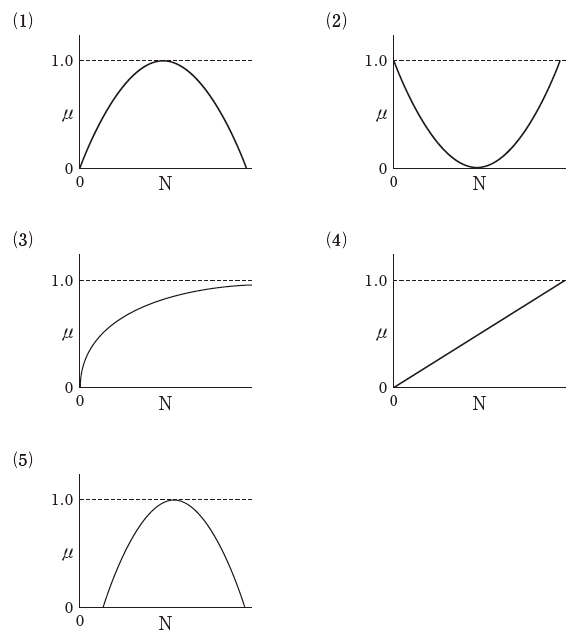
植物プランクトンの栄養塩摂取速度はミハエリス-メンテンの式で記述される。下に示した図で、縦軸は比摂取速度μ(最大で1になる)、横軸は制限となる栄養塩濃度Nとすると、μとNの関係を示す最も適切な図はどれか。
解 説
問題文にもある通り、植物プランクトンの栄養塩摂取速度はミハエリス-メンテンの式で表すことができます。この式は複雑なので正確に記憶しておく必要はなく、特徴を押さえておけば大丈夫です。
まず、重要なパラメータは比摂取速度μと栄養塩濃度Nの2つです。
植物の成長にはある程度の栄養塩が必要なのでこのような名前になっていますが、これを人間に例えると、Nが食卓に並んでいる食べ物の量、μが食べるスピードということになります。以下、人間の食事のスピードについて考えていきます(植物も同様なので)。
まず、食卓に並んでいる食べ物がちょっとしかないときは、貴重なので少しずつ味わって食べると思います。そのため、この場合は食べるスピードは遅いです。次に、食べ物が結構豊富にある場合、遠慮することはないので、それなりにバクバク食べるため、スピードは上がります。とはいえ、食べ放題みたいに膨大な料理があっても、食べるスピードには限界があります。
つまり、最初のうちはN(食べ物の量)が大きくなるにつれてμ(食べるスピード)も大きくなるものの、Nが大きすぎればμはそのうち頭打ちとなります。
ただし、人間と植物では異なる点もあるので注意です。それは、人間の食事は断続的(満腹になったら食事をやめ、空腹になったら食事をとる)ですが、植物の栄養摂取は連続的(土に栄養がある限り摂取を続ける)です。
以上を踏まえて選択肢を見ていきます。
(1)の左半分は悪くありませんが、右半分でN(栄養塩)が多いのにμが小さい(摂取しない)のはおかしいので、これは不適です。
(2)は明らかにおかしくて、Nが0(=栄養がない)のときに、μが1(=栄養を取っている)になるはずがありません。
(3)が正しいグラフです。Nの増加とともにμも対数的に増加し、そのうち頭打ちとなります。
(4)は一見すると(3)と似ていますが、問題文をよく読めばこのグラフは破綻していることがわかります。まず、μは「摂取速度」ではなく「比摂取速度」であり、問題文にも「最大で1」と書かれています。一方で(4)のグラフは右肩上がりになっているので、Nの増大に伴ってμがどこまでも増加するので、これではμに最大値はありません。よって、(4)も不適です(ちなみに、同様のことが(2)にもいえます)。
(5)は(1)と同様の理由で誤っていると判断できますし、栄養塩が多少でもあれば植物は栄養を吸収するので、原点を通っていないことから不適、と判断することもできます。

コメント