H29年 ばいじん・粉じん特論 問6 問題と解説

電気集じん装置の集じん率の推定式であるドイッチェの式として、正しいものはどれか。ただし、ηは集じん率、ω_eは分離速度、Aは有効全集じん面積、Qは処理ガス流量である。

 

 

 

 

 

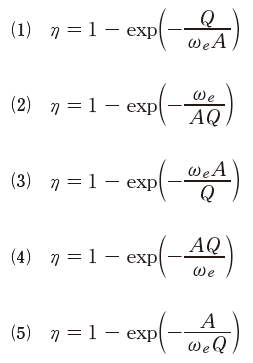
　解 説　　　　

ドイッチェの式というのは、電気集じん装置の集じん率ηの推定式で、以下のように表されます。

• η：集じん率
• ω_e：粒子の分離速度[m/s]
• A：有効集じん面積[m²]
• Q：ガス流量[m³/s]

この公式を知らないと解けない計算問題などもたびたび出題されているので、重要事項としてぜひ押さえておいてください。

よって、(3)が答えになりますが、今回の問題に限っては、公式を覚えていなくても解くことができます。というのも、選択肢の間で異なっている3つの変数(ω_e、A、Q)が大きくなったり小さくなったりしたとき、ηがどう変化するかを考えればよいからです。

その前に、まずは選択肢に出てくる式の説明をします。exp(□)というのは、eの□乗、つまり、e^□を表しています(ちなみに「e」は自然対数の底で、覚えなくて大丈夫ですが、e≒2.7となります)。よって、各選択肢にある3つの変数のうち、分子をx、分母をyとすると、選択肢の式は以下のように書き換えることができます。

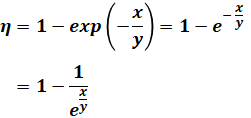
上式を見てわかる通り、xが大きければ、1から引く値の分母が大きくなるので、1から引く値が小さくなります。ということは、集じん率ηは大きくなるということです。

一方、yが大きければ、1から引く値の分母が小さくなるので、1から引く値が大きくなり、ひいては集じん率ηが小さくなります。

要するに、xが大きければηも大きくなり、yが大きければηは小さくなります。

以上を踏まえつつ、ω_e、A、Qについて考えると、分離速度ω_eと有効全集じん面積Aが大きいほど、集じん率ηも大きくなります。反対に、ガス流量Qが多ければ集じん率ηは小さくなります。

よって、ω_eとAは上式のxに当てはまり、Qはyに当てはまります。つまり、選択肢(3)が正解だと判断することができます。