問 題
定格容量500kV・Aの三相変圧器がある。負荷力率が1.0のときの全負荷銅損が6kWであった。このときの電圧変動率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、鉄損及び励磁電流は小さく無視できるものとし、簡単のために用いられる電圧変動率の近似式を利用して解答すること。
- 0.7
- 1.0
- 1.2
- 2.5
- 3.6
解 説
変圧器の電圧変動率については、その定義はともかく、電験三種の試験では以下の近似式を使います(この手の問題では、おそらく毎回、問題文に近似計算を行う旨が記載されます)。そのため、以下の式を公式として覚えておくと良いと思います。
![]()
- ε:電圧変動率[%]
- p:百分率抵抗降下(パーセント抵抗)[%]
- q:百分率リアクタンス降下(パーセントリアクタンス)[%]
- cosθ:力率
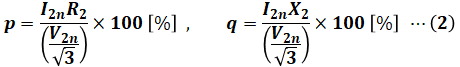
- I2n:定格運転時の二次電流[A]
- R2:二次側に換算した等価回路の抵抗[Ω]
- X2:二次側に換算した等価回路のリアクタンス[Ω]
- V2n:定格運転時の二次電圧[V]
注意点として、(2)式の分母は相電圧を表すので、三相変圧器のときはV2nを√3で割っています。もし単相変圧器として出題された場合には、定格電圧=相電圧なので、(2)式から√3を消してください。
ここで、今回の場合は力率が1.0なので、cosθ=1かつsinθ=0です。よって、(1)式でqsinθ=0となるので、(2)式のqは計算する必要がありません。
問われているのは電圧変動率εなので、百分率抵抗降下pの値を計算するのが当面の目標となります。
ここで、問題文で与えられている条件は定格容量Sn=500[kV・A]と全負荷銅損Pc=6[kW]の2つです。これらを式で表すと、下式のようになります。
![]()
![]()
(3)式と(4)式をうまく(2)式に代入することができれば、分母・分子で約分できてpが求められます。ここでの計算方法は様々なやり方があるので、以下は一例と考えてください。ほかの解き方でも、最終的に答えと一致すれば問題ありません。
まず、(2)式の分母・分子の両方に3I2nを掛けます。そうすると、分母が(3)式を含み、分子が(4)式を含んだ形になります。
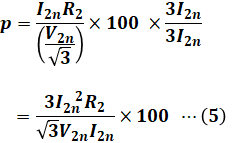
続いて、(5)式に(3)式と(4)式を代入すれば、pが求められます。
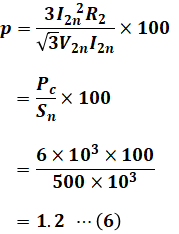
最後に、(6)式を(1)式に代入すれば、求めたい電圧変動率εを計算することができます。
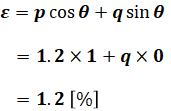
以上から、正解は(3)です。

コメント