電験三種 R3年 電力 問16 問題と解説

　問 題　　　　　

支持点の高さが同じで径間距離150mの架空電線路がある。電線の質量による荷重が20N/m、線膨張係数は1℃につき0.000018である。電線の導体温度が－10℃のとき、たるみは3.5mであった。

次の(a)及び(b)の問に答えよ。ただし、張力による電線の伸縮はないものとし、その他の条件は無視するものとする。

(a)　電線の導体温度が35℃のとき、電線の支持点間の実長の値[m]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 150.18
2. 150.23
3. 150.29
4. 150.34
5. 151.43

(b)　(a)と同じ条件のとき、電線の支持点間の最低点における水平張力の値[N]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 6272
2. 12863
3. 13927
4. 15638
5. 17678

 

 

 

 

 

　解 説　　　　

(a)

電線のたるみに関する計算問題はたびたび出題されているので、以下の2つの式は公式としてぜひ覚えておきたいところです。一つは電線のたるみD[m]を求める式、もう一つは電線の長さL[m]を求める式です。

• D：電線のたるみ [m]
• w：荷重 (電線1mあたり) [N/m]
• S：電線の支持物間の距離 (径間長) [m]
• T：水平張力 (電線の水平方向) [N]

• L：電線の長さ [m]

本問では35℃のときの電線の長さが問われているので、答えを出すには上式のうち(2)式を使うことになります。

ここで、問題文で－10℃のときのたるみが与えられているため、各数値を(2)式に代入します。

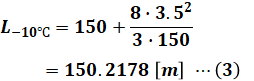
• L_-10℃：－10℃条件下での電線の支持点間の実長の値 [m]

導体の温度が35℃になる場合を考えると、1℃につき、もとの長さの0.000018倍した分だけ膨張するので、次のように計算できます。

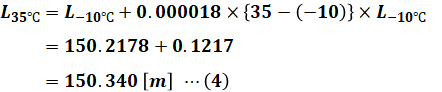
• L_35℃：35℃条件下での電線の支持点間の実長の値 [m]

よって、正解は(4)です。

(b)

問われているのは、35°のときの水平張力の値[N]です。水平張力を使う式は(a)の解説の冒頭で示した(1)式のほうなので、最終的にはこの式を使います。以下に(1)式をもう一度記載します。

• D：電線のたるみ [m]
• w：荷重 (電線1mあたり) [N/m]
• S：電線の支持物間の距離 (径間長) [m]
• T：水平張力 (電線の水平方向) [N]

上式において、求めたいのは水平張力Tです。また、荷重wと径間長Sは問題文で与えられていますが、たるみDは未知数です。そのため、まずはたるみDを計算する必要があります。

たるみDを求めるには、設問(a)でも使った(2)式を用います。(a)では－10℃条件の数値を使いましたが、今回は35℃条件なので、その計算式は以下のようになります。

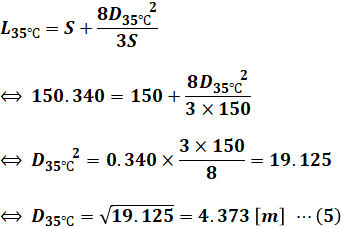
よって、(5)式の結果を(1)式に代入すると、求めたいの水平張力Tを計算することができます。

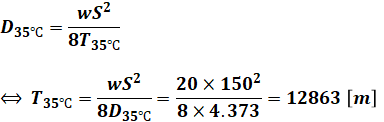
以上から、正解は(2)となります。