電験三種 R2年 機械 問12 問題と解説

　問 題　　　　　

教室の平均照度を500lx以上にしたい。ただし、その時の光源一つの光束は2400lm、この教室の床面積は15m×10mであり、照明率は60%、保守率は70%とする。

必要最小限の光源数として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 30
2. 40
3. 75
4. 115
5. 150

 

 

 

 

 

　解 説　　　　

照度Eは、基本的には、光束Fを面の面積Aで割ったものとして表すことができます。

しかし、実際には部屋に照明器具が複数あるのが普通なので、その個数Nを掛ける必要があります。また、光が壁や床に吸収されてしまう分を考慮した照明率U、経年劣化や汚れによる明るさの減弱を考慮した保守率Mもそれぞれ掛け合わせると、実際に則した平均照度を計算することができます。

よって、最初の式にこれらの条件を付け加えると、作業面における平均照度は以下の式のようになります。この式を使う問題は数年に一度出題されているので、ぜひ覚えておきたい公式です。

• E：平均照度[lx]
• F：光束[lm]
• N：照明の数
• U：照明率
• M：保守率
• A：面積[m²]

上式に問題文で与えられた数値を代入すると、次のようになります。

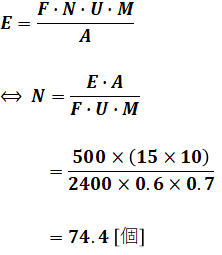
よって、光源の数は計算上は74.4個必要になるので、実際には75個以上なくてはなりません。選択肢(3)にちょうど75個があるので、正解は(3)です。