電験三種 R1年 理論 問18 問題と解説

　問 題　　　　　

図1は、二重積分形A-D変換器を用いたディジタル直流電圧計の原理図で、ある。次の(a)及び(b)の問に答えよ。

(a)　図1のように、負の基準電圧-V_r(V_r＞0)[V]と切換スイッチが接続された回路があり、その回路を用いて正の未知電圧V_x(＞0)[V]を測定する。

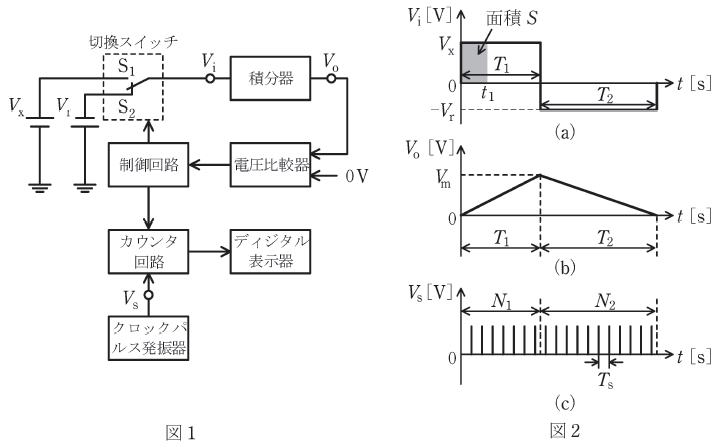
まず、制御回路によってスイッチがS₁側へ切り換わると、時刻t=0sで測定電圧V_x[V]が積分器へ入力される。その入力電圧V_i[V]の時間変化が図2(a)であり、積分器からの出力電圧V_o[V]の時間変化が図2(b)である。ただし、t=0sでの出力電圧をV_o=0Vとする。

時刻t₁におけるV_o[V]は、入力電圧V_i[V]の期間0～t₁[s]で囲われる面積Sに比例する。積分器の特性で決まる比例定数をk(＞0)とすると、時刻t=T₁[s]のときの出力電圧は、V_m=(　ア　)[V]となる。

定められた時刻t=T₁[s]に達すると、制御回路によってスイッチがS₂側に切り換わり、積分器には基準電圧-V_r[V]が入力される。よって、スイッチS₂の期間中の時刻t[s]における積分器の出力電圧の大きさは、V_o=V_m－(　イ　)[V]と表される。

積分器の出力電圧V_oが0Vになると、電圧比較器がそれを検出する。V_o=0Vのときの時刻をt=T₁+T₂[s]とすると、測定電圧はV_x=(　ウ　)[V]と表される。

さらに、図2(c)のようにスイッチS₁、S₂の各期間T₁[s]、T₂[s]中にクロックパルス発振器から出力されるクロックパルス数をそれぞれN₁、N₂とすると、N₁は既知なのでN₂をカウントすれば、測定電圧V_xがディジタル信号に変換される。

ここで、クロックパルスの周期T_sは、クロックパルス発振器の動作周波数に(　エ　)する。

上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

(b)　基準電圧がV_r=2.0V、スイッチS₁の期間T₁[s]中のクロックパルス数がN₁=1.0×10³のディジタル直流電圧計がある。この電圧計を用いて未知の電圧V_x[V]を測定したとき、スイッチS₂の期間T₂[s]中のクロックパルス数がN₂=2.0×10³であった。

測定された電圧V_xの値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.5
2. 1.0
3. 2.0
4. 4.0
5. 8.0

 

 

 

 

 

　解 説　　　　

(a)

(　ア　)に関して、問題文に「V_o[V]は、0～t₁[s]では面積Sに比例する」ということが書かれています。問われているのはV_mですが、これは図2(b)を見てもわかるようにV_oの最大値のことなので、V_mも面積Sに比例するといえます。

また、図2(a)から、面積SはV_xとT₁の積で求めることができるので、V_mはV_x×T₁に比例します。よって、(　ア　)には「kV_xT₁」が入ります。

(　イ　)に関して、0～T₁[s]ではV_oは図2(a)の面積Sに応じて大きくなっていきました。T₁～T₂[s]では、V_oは下図に示す面積S’に応じて小さくなっていくことが図2(b)から読み取れます。

上図より、面積S’はV_rと(t－T₁)の積となるので、(　イ　)には「kV_r(t－T₁)」が入ります。

(　ウ　)で、V_o=0Vとなるのは、図2(a)に示される正の側の面積(V_xT₁)と負の側の面積(V_rT₂)とが等しいときです。よって、次のように計算することができます。

よって、(　ウ　)には「T₂V_r/T₁」が入ります。

(　エ　)では周期T_sと周波数fの関係が問われていますが、周波数というのは1秒間に何周期分あるかということを示すパラメータなので、周期T_sと周波数fとは逆数の関係となります。

よって、(　エ　)には「反比例」が入ります。

以上から、正解は(1)だとわかります。

(b)

問われているのはV_xであり、(a)の(　エ　)で以下の式を得ているので、これを利用してV_xを算出するのがわかりやすいと思います。

ここで、V_rは問題文で与えられている一方、T₁とT₂は未知数ですが、クロックパルスというのは一定のリズムで刻んでいる信号なので、クロックパルス数N₁とN₂の比が、そのままT₁とT₂の比ということになります。

よって、V_xは以下のように計算することで求められます。

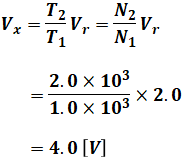
以上から、正解は(4)です。