電験三種 R1年 理論 問2 問題と解説

　問 題　　　　　

図のように、極板間距離d[mm]と比誘電率ε_rが異なる平行板コンデンサが接続されている。極板の形状と大きさは全て同一であり、コンデンサの端効果、初期電荷及び漏れ電流は無視できるものとする。

印加電圧を10kVとするとき、図中の二つのコンデンサ内部の電界の強さE_A及びE_Bの値[kV/mm]の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

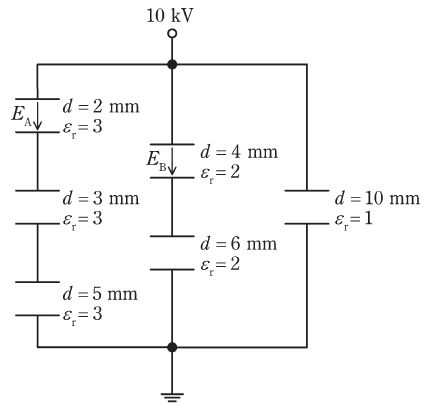
•  E_A　　　E_B

1. 0.25　　0.67
2. 0.25　　1.5
3. 1.0　　  1.0
4. 4.0　　  0.67
5. 4.0　　  1.5

 

 

 

 

 

　解 説　　　　

求めたいのは電界の強さEなので、まずは電界Eと電位Vの関係式を確認しておきます。

問題文にはE_A、E_Bともにdの値が与えられているため、Vの値を計算するのが当面の目標となります。

ここで、問題文には6つのコンデンサが描かれていますが、左側・中側・右側の上下端電圧がそれぞれ10kVになるので、以下では左側と中側を分けて考えます(右側はE_AもE_Bも関係ないので考える必要がありません)。

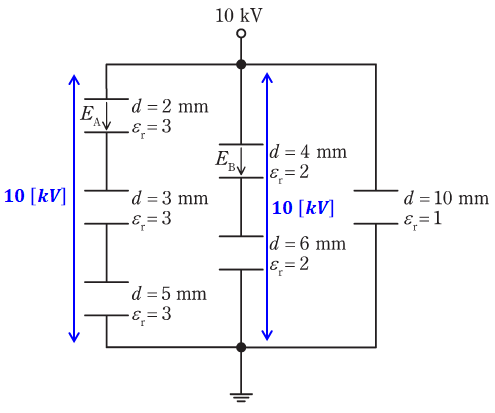
上図左側を見るとコンデンサが直列に3つ並んでいますが、直列に並んだコンデンサに蓄えられる電荷Q[C]は同じ値となります。また、Qは静電容量Cと電圧Vの積で表すことができるので、Qが一定ならCとVは反比例することになります。

• Q：電荷[C]
• C：静電容量[F]
• V：電圧[V]

よって、3つのコンデンサの静電容量Cの比がわかれば、それぞれのコンデンサの電圧Vの比もわかり、合計で10kVというところから各々の電圧Vを計算することができます。

続いて、静電容量Cは以下の式で表すことができます。これも重要公式の一つです。

• ε₀：真空の誘電率[F/m]
• S：極板面積[m²]
• d：極板間の距離[m]

問題の図に描かれた数値を上式に代入すると、次のように計算できます。なお、本来であればdの単位は[m]に直すべきですが、今回は比の計算をしたいだけなので、2[mm]ならそのまま2を代入します(もちろん、きちんと2×10^-3[m]としても構いません)。

よって、Cの比がわかったので、この逆数がVの比ということになります。

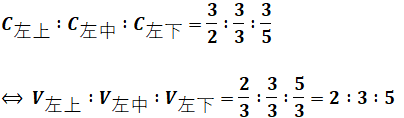
以上から、Vは全体で10[kV]なので、V_左上は次のように計算できます。

これを一番最初に示したE=V/dの式に代入するとE_Aを算出することができます。

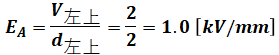
回路図の中側でも同様の計算をすることで、E_Bを求めることができます。以下では簡単にまとめますが、やっていることはE_Aの計算のときと同じです。

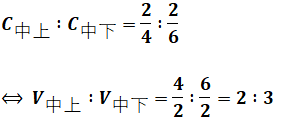
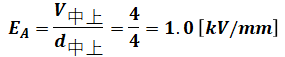
以上から、正解は(3)となります。