前項では論理式について解説するために、論理回路の論理式への変換を紹介しましたが、論理回路から論理式への変換よりも、むしろある論理式を別の論理式に変換するほうが大事です。論理式の変換にはいくつのパターンがあるため、この項では論理式の変換ルールを紹介します。
まず最初に、具体的な変換例を挙げます。このあと一つずつ説明をしていくので、この段階ではなぜこのような変換が可能なのかはわからなくて大丈夫です。
![]()
上式の左辺のような複雑な論理式と、右辺の比較的さっぱりした論理式は全く同じ意味です。以下のルールに従っていけば、左辺を右辺に書き換えることができるようになります。
和の交換、積の交換
普通の算数の四則演算と同様、2つの入力の和や積は、その順序を入れ替えることができます。
![]()
![]()
分配
( )の外に積があるときは、( )内のそれぞれの積とすることで分配が可能です。もちろん、反対も可能です(以下の式で、左辺→右辺に変換しても、右辺→左辺に変換してもよいです)。
![]()
結合
3つ以上の入力の和や、3つ以上の入力の積は、計算する順序を入れ替えることができます。
![]()
![]()
補元
補元という言葉は聞き慣れないかもしれないので、特に名前を覚えておく必要はありません。ルールだけ、しっかり身につけておいてください。補元というのは以下のような式で表されます。
![]()
![]()
1つ目の式は「X」と「Xでないもの」を「OR」でつないでいるので、「Xでも良いし、Xじゃなくても良い」という意味になります。であれば当然、何でも良いことになるので、この出力は必ず1になります。
一方、2つ目の式は、「X」と「Xでないもの」を「AND」でつないでいるので、「Xであり、かつ、Xでないもの」という意味になります。そんなものは存在しないので、これの出力は必ず0になります。
ド・モルガンの定理
これも名前に馴染みがなければ、変換の結果だけ覚えておけば大丈夫です。ド・モルガンの定理というのは以下の式のことをいいますが、つまりは、積の記号にバー(NOT)が付いたら和の記号になり、和の記号にバー(NOT)が付いたら積の記号になるということです。
![]()
![]()
まとめ
以上を踏まえて、最初に提示した式について考えていきます。すると、以下のように段階的にまとめていくことによって、左辺が右辺へと変換できることがわかります。
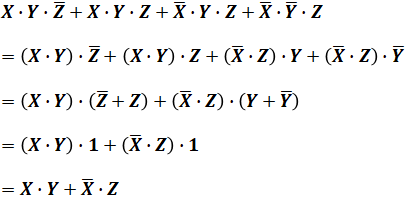

コメント