問 題
次の文章は、直流回路に関する記述である。
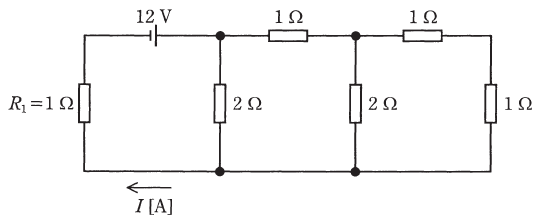
図の回路において、電流の値I[A]は4Aよりも( ア )。このとき、抵抗R1の中で動く電子の流れる向きは図の( イ )であり、電界の向きを併せて考えると、電気エネルギーが失われることになる。
また、0.25sの間に電源が供給する電力量に対し、同じ時間に抵抗R1が消費する電力量の比は( ウ )である。抵抗は、消費した電力量だけの熱を発生することで温度が上昇するが、一方で、周囲との温度差に( エ )する熱を放出する。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ)
- 大きい 上から下 0.5 ほぼ比例
- 小さい 上から下 0.25 ほぼ反比例
- 大きい 上から下 0.25 ほぼ比例
- 小さい 下から上 0.25 ほぼ反比例
- 大きい 下から上 0.5 ほぼ反比例
解 説
まず( ア )に関しては、4Aよりも大きいか小さいかで考えるよりも、具体的な電流値を計算したほうが早いと思います。問題の回路にある抵抗に、以下のような番号を振って解説します。
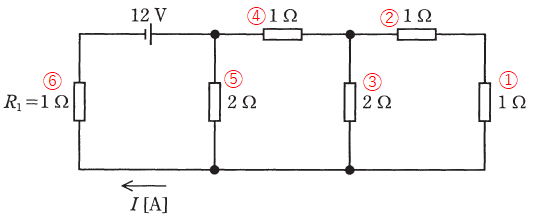
抵抗①と②は直列に並んでいるため、これらの合成抵抗は単純な和で、1+1=2[Ω]となります。また、その合成抵抗と③とは並列接続になるため、その合成抵抗は以下のような計算によって、1[Ω]と求めることができます。
![]()
続いて、これと④とは直列接続なので、その合成抵抗は、1+1=2[Ω]です。さらに、⑤とは並列になっているので、先程と同様の計算によりここまでの合成抵抗は1[Ω]となります。
![]()
最後に⑥との直列接続の結果、最終的な合成抵抗は、1+1=2[Ω]となります。
よって、電源を流れる電流Iの大きさは、
![]()
となるので、( ア )の答えは、4Aよりも「大きい」となります。
( イ )について、電流Iは上記の計算の通り、図の矢印の向きに6Aで流れています。よって、抵抗R1(解説の図では⑥)のところを電流は下から上へと流れていることになります。電子の流れの向きは電流とは常に反対であるため、( イ )には「上から下」を入れるのが適切です。
( ウ )を含む文章では0.25sという時間に関する数値が出てきていますが、これには特に意味がありません(電力量を供給する時間と消費する時間がどちらも同じであるため)。
抵抗R1(解説の図では⑥)とそれ以外((1)~(5))の合成抵抗を分けて図示すると、以下のような回路図が描けます。
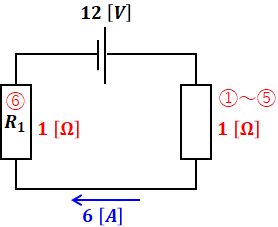
上図の(1)~(5)の合成抵抗と、抵抗R1(上図の⑥)はどちらも同じ1[Ω]なので、これらの消費電力量は等しいはずです。ということは、電源で供給する電力量を1とすれば、抵抗R1で消費される電力量はその半分の0.5となります。よって、( ウ )には「0.5」が入ります。
( エ )の選択肢は「ほぼ比例」か「ほぼ反比例」の2択ですが、温度差が大きいほど放出する熱量が小さいというのはおかしいです。もしそうなら、抵抗の温度と周囲の温度とがほぼ同じ場合、分母が0になって爆発的な(数字の上では無限大の)熱量が放出されるということになってしまいます。
もちろん、実際にはそんなはずもなく、熱量は温度差に「ほぼ比例」するのが正解です。

コメント