問 題
次の論理回路について、(a)及び(b)の問に答えよ。
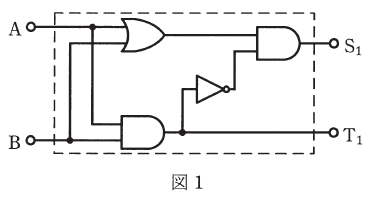
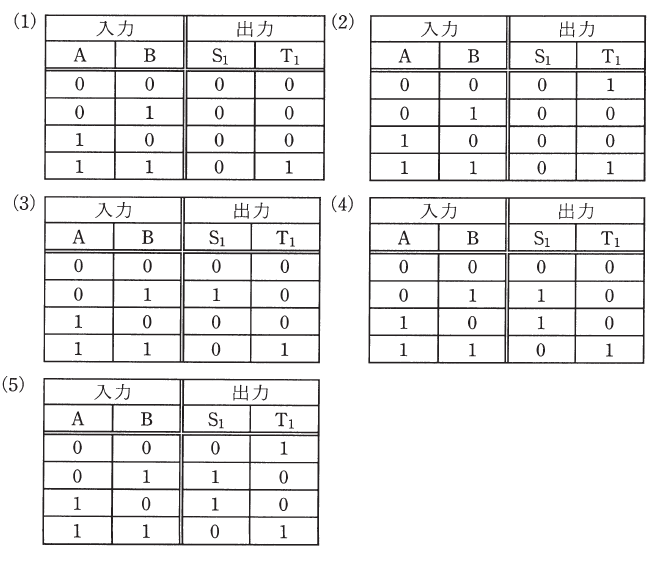
(a) 図1に示す論理回路の真理値表として、正しいものを次の(1)~(5)のうちから一つ選べ。
(b) 図1に示す論理回路を2組用いて図2に示すように接続して構成したとき、A、B及びCの入力に対する出力S2及びT2の記述として、正しいものを次の(1)~(5)のうちから一つ選べ。
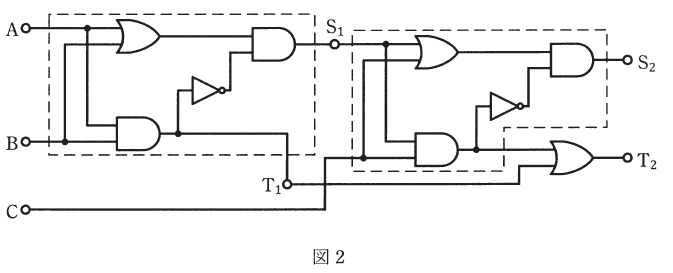
- A=0、B=0、C=0を入力したときの出力は、S2=0、T2=1である。
- A=0、B=0、C=1を入力したときの出力は、S2=0、T2=1である。
- A=0、B=1、C=0を入力したときの出力は、S2=1、T2=0である。
- A=1、B=0、C=1を入力したときの出力は、S2=1、T2=0である。
- A=1、B=1、C=0を入力したときの出力は、S2=1、T2=1である。
解 説
(a)
まず、解説しやすいように、図1のそれぞれのポイントに以下のようにアルファベットを振ります。
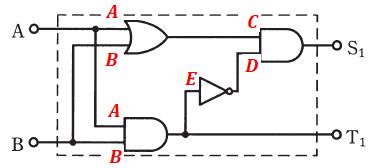
上図を見るとわかるように、S1はCとDの積で、そのCはAとBの和、他方のDはEの否定で、EはAとBの積であることがわかります。よって、これを式で表すと、次のように書くことができます。
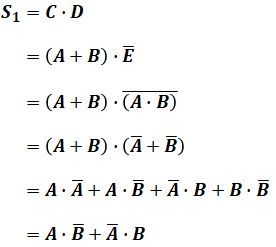
これはつまり、AとBが反対同士であれば、S1が1となる、という意味になります。反対に、AとBが同じなら、S1は0となるということです。
最後から2番目の式が最後の式に変換できるのは、「Aであり、かつ、Aでない」や「Bであり、かつ、Bでない」という事象は有り得ないため、この項を消して(0として)いるからです。
一方、T1はAとBの積になっているので、その式も単純です。
![]()
以上を踏まえて選択肢を見ていきます。
先に考えやすそうなT1を扱うと、T1(=A・B)が1になるためには、AもBも1でなくてはいけません。選択肢(1)~(5)の全てがこれを満たしていますが、(2)と(5)では、AとBがともに1でない部分でもT1が1となっている箇所があります。よって、(2)と(5)は誤りです。
続いてS1を考えますが、上で解説した通り、AとBの値が異なるならS1は1となり、2つの値が同じならS1は0になります。(1)、(3)、(4)の選択肢の中でこれを満たすのは(4)だけなので、正解は(4)だと判断できます。
以上から、正解は(4)となります。
なお、別解として、真理値表を使った方法ではなく代入法で解くこともできます。そのやり方については、類題であるR4年度上期 問18の解説で紹介しているので、必要に応じて参照し、ご自分に合った解法を採用してください。
(b)
図2の左側は図1と全く同じで、右側は図1でいうAの位置がS1、Bの位置がC、S1の位置がS2で、T1の位置は何も書いていないのでT3とします。
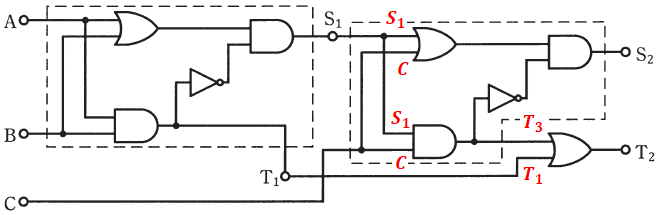
すると、左側の点線枠内と右側の点線枠内の真理値表は次のように表されます。左側は(a)の答えそのままで、右側はアルファベットだけ変えていますが、論理回路の構成が同じなので値の並びは変わりません。
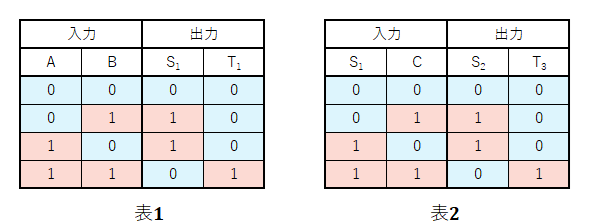
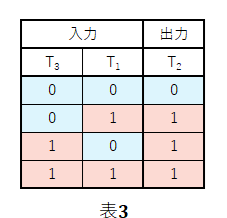
また、T2の値を求めるための真理値表は次のようになります。
以上を踏まえて、選択肢を見ていきます。
(1)はA=0、B=0、C=0なので、表1よりS1=0、T1=0で、表2を見るとS2=0、T3=0となり、表3からT2=0と判断できます。よって、これは誤りの選択肢です。
(2)はA=0、B=0、C=1なので、表1よりS1=0、T1=0で、表2を見るとS2=1、T3=0となり、表3からT2=0と判断できます。よって、これは誤りの選択肢です。
(3)はA=0、B=1、C=0なので、表1よりS1=1、T1=0で、表2を見るとS2=1、T3=0となり、表3からT2=0と判断できます。よって、これが正しい選択肢です。
(4)はA=1、B=0、C=1なので、表1よりS1=1、T1=0で、表2を見るとS2=0、T3=1となり、表3からT2=1と判断できます。よって、これは誤りの選択肢です。
(5)はA=1、B=1、C=0なので、表1よりS1=0、T1=1で、表2を見るとS2=0、T3=0となり、表3からT2=1と判断できます。よって、これは誤りの選択肢です。
以上から、正解は(3)となります。
なお、設問(a)と同様、論理式を使った方法ではなく代入法で解くこともできます。そのやり方については、類題であるR4年度上期 問18の解説で紹介しているので、必要に応じて参照し、ご自分に合った解法を採用してください。

コメント