電験三種 H28年 機械 問9 問題と解説

　問 題　　　　　

図は、2種類の直流チョッパを示している。いずれの回路もスイッチS、ダイオードD、リアクトルL、コンデンサC(図1のみに使用されている。)を用いて、直流電源電圧E=200Vを変換し、負荷抵抗Rの電圧v_d1、v_d2を制御するためのものである。

これらの回路で、直流電源電圧はE=200V一定とする。また、負荷抵抗Rの抵抗値とリアクトルLのインダクタンス又はコンデンサCの静電容量の値とで決まる時定数が、スイッチSの動作周期に対して十分に大きいものとする。

各回路のスイッチSの通流率を0.7とした場合、負荷抵抗Rの電圧v_d1、v_d2の平均値V_d1、V_d2の値[V]の組合せとして、最も近いものを次の(1)～(5)のうちから一つ選べ。

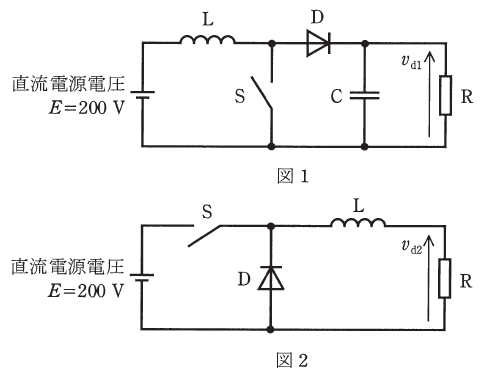
　　　V_d1V_d2

1. 667　　140
2. 467　　60
3. 667　　86
4. 467　　140
5. 286　　60

 

 

 

 

 

　解 説　　　　

図1は直流チョッパの中でも、直流昇圧チョッパの回路図です。

スイッチがオンの状態だと、回路図の左側で電流がぐるぐる廻るので、インダクタンスLにエネルギーが蓄積されます。その状態でスイッチをオフにすると、今度はインダクタンスLに逆起電力が発生し、蓄積されたエネルギーを放出するかたちとなって負荷側に電流が流れるので、電源電圧よりも高い電圧が負荷抵抗Rにかかることになります。

スイッチオンでエネルギーを溜めて、スイッチオフでそれを放出するので、オフ時間が短い(オン時間が長い)ほど昇圧の程度が大きくなります。

それを式で表すと、次のように書くことができます。

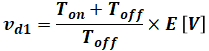
• T_on：スイッチオンの時間
• T_off：スイッチオフの時間

よって、今回はスイッチの通流率が0.7ということなので、T_on=0.7、T_off=0.3と考えることができるので、次のように計算できます。

一方、図2は直流降圧チョッパの回路図です。

この回路では、スイッチをオンにすると、負荷抵抗Rに電流が流れつつ、インダクタンスLにエネルギーが蓄えられます。このあとスイッチをオフすると、電源側は切り離されますが、インダクタンスLに蓄えられたエネルギーがあるので、図2の右側半分の回路を電流が循環します。

よって、常にスイッチオンでv_d2=Eであり、オフ時間の割合が増えるとともに降圧の程度が大きくなるので、式で表すと次のようになります。

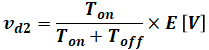
よって、問題文の数値を代入すると、次のように計算できます。