問 題
十分長いソレノイド及び小さい三角形のループがある。図1はソレノイドの横断面を示しており、三角形ループも同じ面内にある。図2はその破線部分の拡大図である。面x=0から右側の領域(x>0の領域)は直流電流を流したソレノイドの内側であり、そこには+z方向の平等磁界が存在するとする。その磁束密度をB[T](B>0)とする。
一方、左側領域(x<0)はソレノイドの外側であり磁界は零であるとする。ここで、三角形PQRの抵抗器付き導体ループがxy平面内を等速度u[m/s]で、+x方向に進み、ソレノイドの巻線の隙間から内側に侵入していく。その際、導体ループの辺QRはy軸と平行を保っている。頂点Pが面x=0を通過する時刻をT[s]とする。また、抵抗器の抵抗r[Ω]は十分大きいものとする。
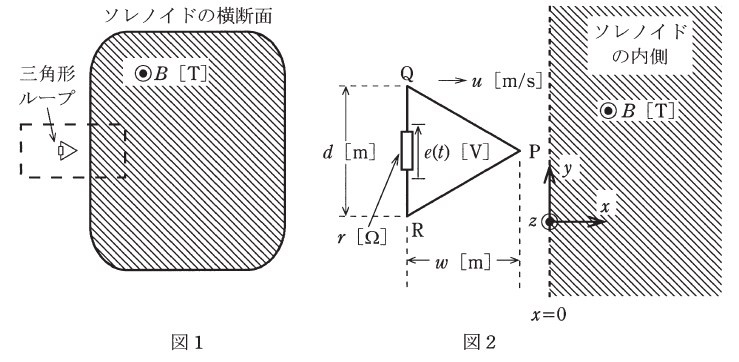
辺QRの中央の抵抗器に時刻t[s]に加わる誘導電圧をe(t)[V]とし、その符号は図中の矢印の向きを正と定義する。三角形ループがソレノイドの外側から内側に入り込むときのe(t)を示す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。
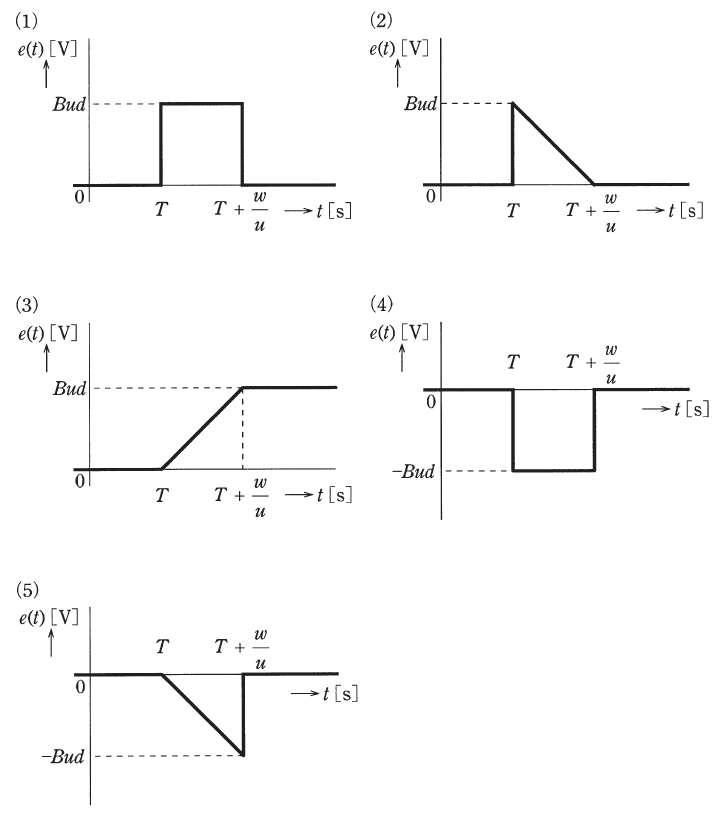
解 説
まず、誘導電圧(誘導起電力)は、磁界の変化に応じて発生するものです。磁界それ自身ではなく磁界の変化が必要なので、三角形ループがソレノイドに侵入する前(0<t<T)はもちろん誘導電圧が発生しない上、三角形ループが全て入りきったあと(T+w/u<t)も、誘導電圧は0となります。この時点で、選択肢(3)が誤りであるとわかります。
問題はその途中である「T<t<T+w/u」の範囲ですが、誘導電圧の大きさと向きをフレミングの右手の法則から考えます。
フレミングの右手の法則とは、長さl[m]の導体を磁束密度B[T]の磁束の方向と直角に置き、速度v[m/s]で導体と磁束の両方に直角な方向に移動させると、導体にe=Blv[V]の誘導起電力が発生するという法則です。その向きは、親指と人差し指と中指を全て直角に配置した状態のとき、中指=起電力、人差し指=磁束、親指=運動の向きとなります。
今回の場合は、磁束密度Bの向きが画面(紙面)奥側から手前側で、運動方向は左側から右側なので、誘導電圧の向きは上から下向きになります。よって、問題文の図に記入されているeの矢印とは反対向きなので、負の誘導電圧が発生することになるため、選択肢(4)と(5)のどちらかが正解となります。
上記の通り誘導電圧の大きさはe=Blv[V]となりますが、Bは定数で、v(今回の問題ではu)も定数です。残るlは図2でいうx=0の線と、三角形PQRとが重なる線の長さになります。つまり、三角形ループがソレノイドにちょうど侵入したときは点Pが重なっているだけなのでl=0で、その後徐々に大きくなり、最終的に辺QRの長さであるl=dとなります。
よって、eは0から始まってe=Budまで直線的に増加しているので、選択肢(5)が正しいことがわかります。

コメント