電験三種 H25年 理論 問2 問題と解説

　問 題　　　　　

図のように、真空中の直線上に間隔r[m]を隔てて、点A、B、Cがあり、各点に電気量Q_A=4×10^-6[C]、Q_B[C]、Q_C[C]の点電荷を置いた。これら三つの点電荷に働く力がそれぞれ零になった。このとき、Q_B[C]及びQ_C[C]の値の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

ただし、真空の誘電率をε₀[F/ｍ]とする。

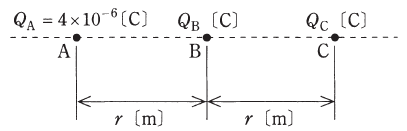
　　　Q_BQ_C

1. 1×10^-6 -4×10^-6
2. -2×10^-68×10^-6
3. -1×10^-64×10^-6
4. 0　　　　　-1×10^-6
5. -4×10^-61×10^-6

 

 

 

 

 

　解 説　　　　

まずQ_BとQ_Cの符号について考えると、Q_Bがマイナス、Q_Cがプラスであるとわかります。その理由は、点Aに働く力が0になるためにはQ_BとQ_Cの符号が逆でなくてはいけないことと、もしQ_Bがプラス、Q_Cがマイナスだったら、点Cは同じ側(紙面左側)に同符号の電荷を持つので、点Cに働く力が0にならないためです。

あとは各点で働く力について計算していきます。2つの点電荷(大きさを持たない電荷)の間にはたらく静電気力は以下の式で示されます。

• F：静電気力[N]
• ε₀：真空の誘電率 8.854×10^-12[F/m]
• Q：電荷[C]
• r：電荷間の距離[m]

点Aについて考えると、F_B=F_Cとなるため、

となり、同様に点Bについて考えると、F_A=F_Cとなるため、

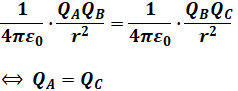
になります。あとはこれらを組み合わせて連立方程式を解けば、

Q_B=-1×10^-6

Q_C=4×10^-6

と答えができます。