問 題
図の回路のスイッチを閉じたあとの電圧v(t)の波形を考える。破線から左側にテブナンの定理を適用することで、回路の時定数[s]とv(t)の最終値[V]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、初めスイッチは開いており、回路は定常状態にあったとする。
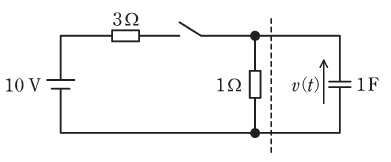
- 時定数[s] 最終値[V]
- 0.75 10
- 0.75 2.5
- 4 2.5
- 1 10
- 1 0
解 説
RC直列回路における時定数τの式は、以下のように表すことができます。
![]()
これは重要事項として押さえておきたい公式ですが、今回はRC直列回路ではない点に注意が必要です。回路図を見ると、左側に抵抗が一つと、右側には抵抗とコンデンサが並列に並んでいます。そのため、この回路図をRC直列回路に直すのが最初の課題です。
問題の回路図をRC直列回路に直すために使うのが、問7の解説でも使用したテブナンの定理です。問7の場合はテブナンの定理を使わずに解いても構いませんが、今回はわざわざ問題文で指定しているので、素直に従うべきだと思います。
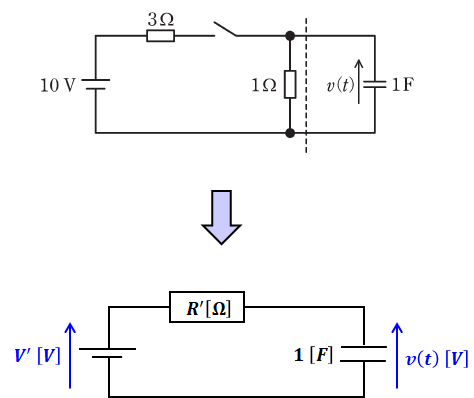
テブナンの定理を使えば、目的とする抵抗(コンデンサなどでも可)以外の部分を1つの抵抗と1つの電源に置き換え、下図下側のような簡単な等価回路に変換することができます。
テブナンの定理の詳細な説明は鳳・テブナンの定理(実践)のページを読んでほしいのですが、簡単にまとめると以下の4ステップで構成されます。
- 目的の抵抗(今回はコンデンサ)の両端で断線させる
- 1の状態で、断線させた両端の電圧差が合成電源V’となる
- 2の状態から、全ての電圧源を短絡させる
- 3の状態で、残った抵抗の合成抵抗がR’となる
ステップ1の結果を図示すると以下の図のようになります。
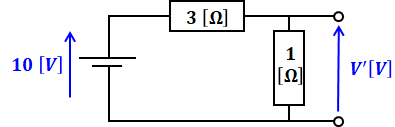
ステップ2で、上図は3[Ω]と1[Ω]の直列回路なので、断線させた両端の電圧差を求めるには次のような計算を行えばよいです。
![]()
ステップ3を考えると、次のような回路図が描けます。
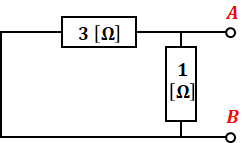
ステップ4では上図を元に合成抵抗R’を求めますが、このとき、最初にコンデンサがあった場所(回路図の右側)の端子から見た合成抵抗R’を求める必要があります。
つまり、上図A点を起点としてB点を終点とする(逆でも可)道すじの合成抵抗です。よって、3[Ω]と1[Ω]の2つの抵抗は並列に並んでいるため、合成抵抗は次のように計算できます。
![]()
以上でV’とR’がわかったので、問題の回路はテブナンの定理によって次のように描き換えることができます。
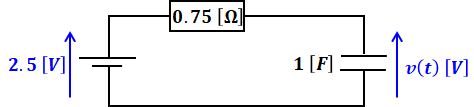
よって、時定数τは次のようになるため、正解は(1)か(2)に絞られます。
![]()
続いて、上図の回路(テブナンの定理を使った回路)を見るとわかるように、この状態で十分な時間が経過すればコンデンサが最大まで充電されるため、これ以上電流が流れなくなります。回路に電流が流れないということは抵抗の両端の電圧差は0になるため、電源電圧がそのままコンデンサの両端の電圧差に相当します。
よって、v(t)の最終値はこの回路図における電源電圧と同じ2.5[V]となります。
以上から、正解は(2)です。

コメント