前項では、下図左側のような複雑な回路でも、鳳・テブナンの定理を使えば、目的とする抵抗R以外の部分を1つの抵抗と1つの電源に置き換え、下図右側のような簡単な等価回路に変換できることを紹介しました。
(前項を読んでいない方へ:ここでの目的は、下図左側の回路において抵抗Rを流れる電流Iを知ることです。)
この項では、この変換の仕方について解説します。
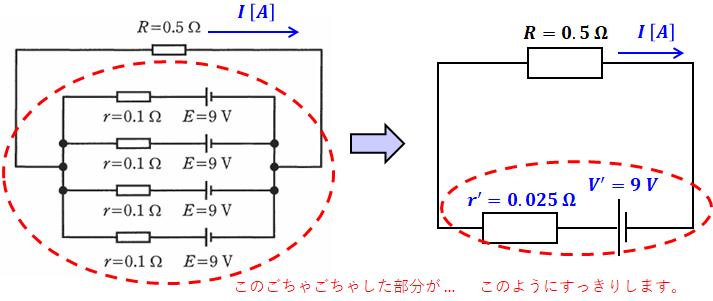
鳳・テブナンの定理によって抵抗と電源を1つずつにまとめることができますが、上図右側における合成電源V’と合成抵抗r’はそれぞれ違う計算方法によって求める必要があります。
まず、合成電源V’の求め方について説明します。最初に上図左側の回路に対し、目的の箇所(今回は抵抗R)の両端で断線させて、これを含まない側の回路について考えます。つまり、以下のような回路からスタートします。
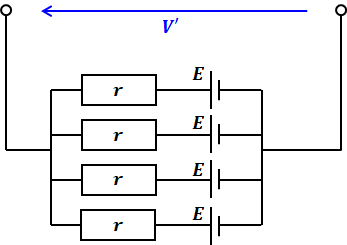
上図において、断線させた両端の電圧差が求めたいV’に相当します。上図の回路において、rに流れる電流が0なので、V’=E=9[V]となります。
もし断線によってrに電流が流れなくなるということが感覚的に納得できない場合は、rに流れる電流をI’として考えてください。4つのrは等価な環境にあるため、1つのrに流れる電流がI’であれば、ほかのrに流れる電流の大きさも向きも一緒のはずです。
しかし、それでは4つのrの合流地点に流れる電流は4I’になるはずですが、その先は断線しているため、電流が流れる余地はありません。よって、4I’=0⇔I’=0となり、結局、rの両端の電位差は0なので、V’=Eとなります。
以上でV’がわかったので、続いてr’を求め方について解説します。r’を求めるには、上図において電源となる部分(今回は4つのE)を全て無いものと考えて(つまり短絡させて)、残った抵抗で計算した合成抵抗の値がr’に相当します。
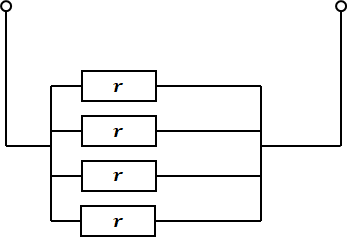
この問題では上図のように4つの等価な抵抗rが並行に並ぶので、その合成抵抗r’は、
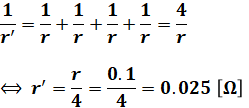
となります。
以上を組み合わせると、鳳・テブナンの定理を適用したあとの回路は次のようにまとめることができます。
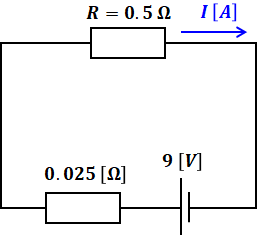
よって、Rを流れる電流Iは
![]()
というように計算することができます。
繰り返しになりますが、鳳・テブナンの定理は、ごちゃごちゃした(複雑な)電気回路において、ある1箇所での電流値や電圧を求める際に便利な定理です。
どんなに複雑な回路でも、目的とする「ある1箇所」(の抵抗など)以外の部分を、1つの抵抗と1つの電源に変換できるので、キルヒホッフの法則で解こうとすると計算が煩雑になりそうな場合は、この定理を使うことを思い出してください。

コメント