問 題
三相3線式高圧配電線で力率cosφ1=0.76(遅れ)、負荷電力P1[kW」の三相平衡負荷に電力を供給している。三相平衡負荷の電力がP2[kW]、力率がcosφ2(遅れ)に変化したが線路損失は変わらなかった。
P1がP2の0.8倍であったとき、負荷電力が変化した後の力率cosφ2(遅れ)の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、負荷の端子電圧は変わらないものとする。
- 0.61
- 0.68
- 0.85
- 0.90
- 0.95
正解 (5)
解 説
問題文に条件が変化する前後で線路損失が変わらなかったと書いてあるので、まずは線路損失Plossの式を以下に示します。
![]()
- Ploss:線路損失[W]
- I線:線電流[A]
- R:線路抵抗[Ω]
一方、三相3線式の負荷電力Pは以下の式で表すことができます。
![]()
- P:負荷電力[W]
- V相:相電圧[V]
- I相:相電流[A]
- V線:線間電圧[V]
- I線:線電流[A]
- cosφ:力率
今回は線路抵抗の式で線電流を用いているため、上式でも線電流を含むほうを使います。
![]()
ここで、これらの式に出てくるパラメータのうち、何が変数で何が定数かを確認しておきます。Plossは問題文の条件より不変なので定数として扱えます。RとV線は電線を変えるわけではないので定数です。一方、P、I線、φは変数になります。
(1)式において、Plossは一定なので、条件の変化前後で以下のような式が成り立ちます。文字式の右下の1,2は、問題文のφやPに付いている1,2と連動していると考えてください。

また、(2)式は負荷電力P1とP2に分けて考えると、それぞれ以下のような式で表すことができます。
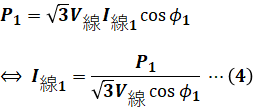
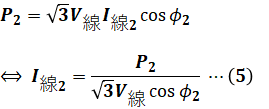
(4)式と(5)式を(3)式に代入すると、次のようになります。
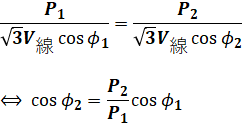
よって、あとは問題文で与えられた数値を代入していけば答えを求めることができます。
![]()
以上から、正解は(5)となります。

コメント