問 題
エミッタホロワ回路について、次の(a)及び(b)の問に答えよ。
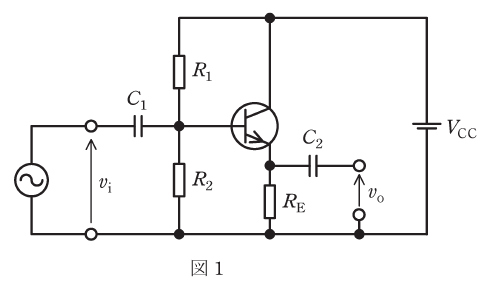
(a) 図1の回路でVCC=10V、R1=18kΩ、R2=82kΩとする。動作点におけるエミッタ電流を1mAとしたい。抵抗REの値[kΩ]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、動作点において、ベース電流はR2を流れる直流電流より十分小さく無視できるものとし、ベース-エミッタ間電圧は0.7Vとする。
- 1.3
- 3.0
- 7.5
- 13
- 75
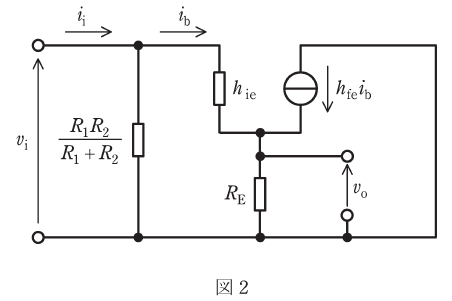
(b) 図2は、エミッタホロワ回路の交流等価回路である。ただし、使用する周波数において図1の二つのコンデンサのインピーダンスが十分に小さい場合を考えている。
ここで、hie=2.5kΩ、hfe=100であり、REは小問(a)で求めた値とする。入力インピーダンス![]() の値[kΩ]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、viとiiはそれぞれ図2に示す入力電圧と入力電流である。
の値[kΩ]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、viとiiはそれぞれ図2に示す入力電圧と入力電流である。
- 2.5
- 15
- 80
- 300
- 750
解 説
(a)
問題文で与えられた条件を図1に書き込むと、下図のようになります。
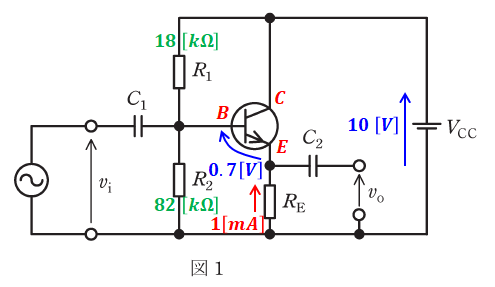
求めたいのはREですが、図から、REの端子間電圧と0.7[V]の和がR2の端子間電圧と一致することがわかります。よって、まずはR2の端子間電圧を求めます。
R1の端子間電圧とR2の端子間電圧の和がVCC=10[V]であるため、R2の端子間電圧VR2は以下のように計算することができます。
![]()
よって、次のように計算することでREを導出できます。
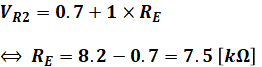
なお、本来であればオームの法則を使う際には抵抗の単位を[kΩ]から[Ω]に変換しておくべきです。しかし、今回は電流の単位が[mA]になっているため、抵抗[kΩ]と電流の[mA]の積がちょうど[V]となるので、そのままでも問題なく計算を進めることができます。
もちろん、このやり方に違和感を覚えるのであれば、一度[kΩ]を[Ω]に変えてから計算をしても全く構いません。
(b)
図2に描かれている「◯に横線」は電流源の記号です。電流源を流れる電流はhfeib[A]で表されます。今回はhfe=100なので、抵抗REには左上から電流ibが、右上から電流100ibが流れ込むため、ここには計101ib[A]の電流が流れることになります。
これを踏まえて図2の回路図を描き換えると、以下のような回路図となります。
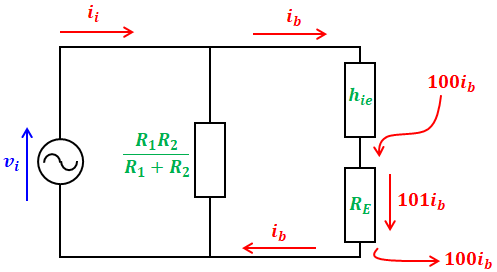
求めたいのは![]() ですが、上図のうち未知数はvi、ii、ibの3つだけなので、どうにか2つの等式を作って連立方程式を解けば、ibを消せるので答えとなる比を求めることができそうです。
ですが、上図のうち未知数はvi、ii、ibの3つだけなので、どうにか2つの等式を作って連立方程式を解けば、ibを消せるので答えとなる比を求めることができそうです。
2つの等式の立て方はいくつかのパターンが考えられますが、ここでは単純そうなものを選んで紹介します。
まず、上図回路の右側にある2つの抵抗に注目してください。hieを流れる電流はibで、REを流れる電流は101ibです。そして両方の抵抗を合わせた端子間電圧は電源電圧のviとなります。よって、以下の等式が成り立ちます。
![]()
上式に対し、わかっている数値を代入していくと次のように計算できます。(a)のときと同様、電流の単位は[mA]、抵抗の単位は[kΩ]として考えることで、いちいち×10-3などを入れなくて済みます。
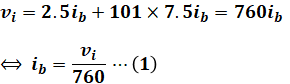
続いて、上図回路の中央に注目してください。ここの抵抗も端子間電圧は電源電圧のviとなります。よって、以下の等式が成り立ちます。
![]()
ここでも先程と同じように、できるだけ数値を代入して整理します。
![]()
ここで、(1)式を(2)式に代入することで、ibを消します。
![]()
あとは求めたい![]() に合うような形で式変形を行えば、答えを出すことができます。
に合うような形で式変形を行えば、答えを出すことができます。
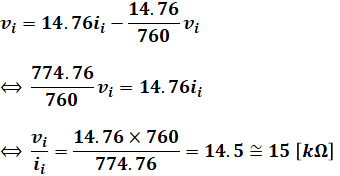

コメント