電験三種 H29年 電力 問8 問題と解説

　問 題　　　　　

支持点間が180m、たるみが3.0mの架空電線路がある。

いま架空電線路の支持点間を200mにしたとき、たるみを4.0mにしたい。電線の最低点における水平張力をもとの何[%]にすればよいか。最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、支持点間の高低差はなく、電線の単位長当たりの荷重は変わらないものとし、その他の条件は無視するものとする。

1. 83.3
2. 92.6
3. 108.0
4. 120.0
5. 148.1

 

 

 

 

 

　解 説　　　　

電線のたるみに関する計算問題はたびたび出題されているので、以下の2つの式は公式としてぜひ覚えておきたいところです。一つは電線のたるみD[m]を求める式、もう一つは電線の長さL[m]を求める式です。

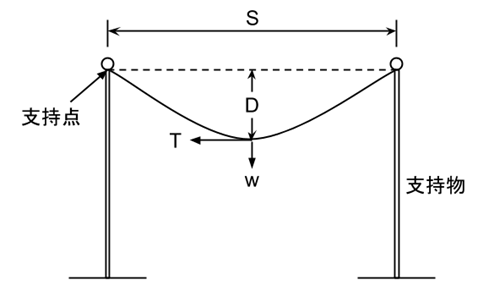
• D：電線のたるみ[m]
• w：荷重(電線1mあたり)[N/m]
• S：電線の支持物間の距離(径間長)[m]
• T：水平張力(電線の水平方向)[N]

• L：電線の長さ[m]

今回はこのうち、たるみDの式を使います。最初の条件はS=180、D=3.0なので、これを上式に代入してTについて解くと、

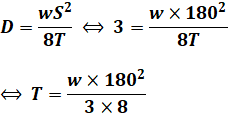
となります。

続いて、S=200、D=4.0のときの張力をT’とすると、

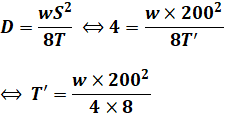
となります。

以上から、その比を計算すると、

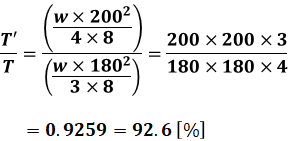
となるため、正解は(2)です。