問 題
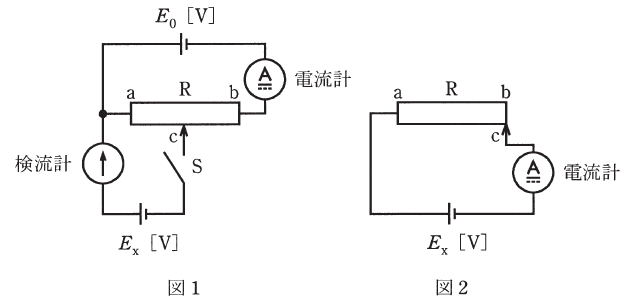
図のように、a-b間の長さが15cm、最大値が30Ωのすべり抵抗器R、電流計、検流計、電池E0[V]、電池Ex[V]が接続された回路がある。この回路において次のような実験を行った。
実験Ⅰ:図1でスイッチSを開いたとき、電流計は200mAを示した。
実験Ⅱ:図1でスイッチSを閉じ、すべり抵抗器Rの端子cをbの方向へ移動させて行き、検流計が零を指したとき移動を停止した。このときa-c間の距離は4.5cmであった。
実験Ⅲ:図2に配線を変更したら、電流計の値は50mAであった。
次の(a)及び(b)の問に答えよ。
ただし、各計測器の内部抵抗及び接触抵抗は無視できるものとし、また、すべり抵抗器Rの長さ[cm]と抵抗値[Ω]とは比例するものであるとする。
(a) 電池Exの起電力の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1.0
- 1.2
- 1.5
- 1.8
- 2.0
(b) 電池Exの内部抵抗の値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.5
- 2.0
- 3.5
- 4.2
- 6.0
解 説
(a)
実験Ⅰではスイッチを開いているので、図1の下半分は関係なく上半分の回路として考えることができます。E0が未知数でRが30[Ω]、電流Iが200[mA]なので、E0は次のように計算できます。
![]()
実験Ⅱではスイッチを閉じるので図1の下半分を考慮する必要があり、図1の等価回路を描くと次のようになります。すべり抵抗器を点cで2つに分けた点と、電池EXの内部抵抗を図示した点に注意してください(電池EXの内部抵抗は設問(a)では使いませんが、設問(b)で考える必要が出てきます)。
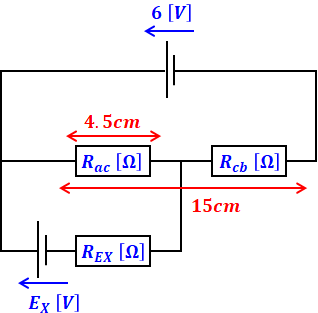
ここで、実験ⅡではRacの端子電圧とRcbの端子電圧の合計が6[V]となるので、Racの端子電圧Vacは抵抗の長さから、
![]()
と計算できます。
また、Vac=1.8[V]であれば上図の回路より、Exの起電力と内部抵抗を含めたEx全体の端子電圧も1.8[V]となりますが、今回は検流計の値が0(Exに電流が流れていない)なので、内部抵抗は無視することができるため、Exの起電力がそのまま1.8[V]ということになります。
(b)
実験Ⅲの図2を電池EXの内部抵抗REXがわかりやすいように描き変えると次のようになります。
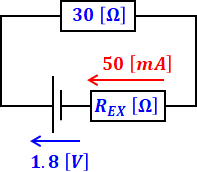
よって、REXは以下のように計算して求めることができます。
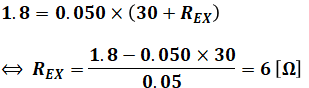

コメント