2の3乗は2×2×2=8、といったように、数値を累乗のかたちで扱うのが指数です。より正確には、◯乗の◯の部分が指数です。2の3乗の場合は「3」が指数となります。また、「23」のように指数を含んだ値のことを累乗数といいます。
とはいえ、この名称を正確に抑えなくても、別に問題はありません。電験三種の計算問題において指数を使う際には、0乗の意味、マイナス乗の意味、5つの指数法則を覚えておけば大丈夫です。
押さえておくべきこれらのことを、以下にひとつずつ示していきます。
0乗
ある値aを0乗すると、aの値(元の値)に関わらず、0乗したあとの数値は1になります。
![]()
つまり、2の0乗も、3の0乗も、5の0乗も、全て1となります。
マイナス乗
ある値aの指数がマイナスになっている場合、分母と分子を反対にすることによって、マイナスを消すことができます。
![]()
例: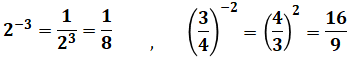
重要な指数法則5パターン
指数の計算には様々なパターンがありますが、基本的には以下の5パターンを押さえておけば、電験三種の計算問題を解く際には充分だと思います。逆に、この5つを知らないと、計算が進まない、もしくは、遠回りで面倒な計算を強いられることになるかもしれません。
①:![]()
例①:![]()
②:![]()
例②:![]()
③:![]()
例③:![]()
④:![]()
例④:![]()
⑤:![]()
例⑤: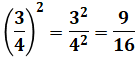
上記5式はいずれも左辺と右辺が等式(イコール)で結ばれています。よって、左辺の形を見たら右辺の形に式変形できるようにするのはもちろんのこと、必要に応じて、右辺を左辺に変えることもできます。

コメント