前項で扱った指数と対の関係にあるのが、この項で解説する対数です。2の3乗はいくつだろう…と考えるのが指数で、それを式で表すと次のようになります。
![]()
一方、2を何乗したら8になるんだろう…という、◯乗の部分を考えるのが対数で、以下の式のように表します。
![]()
これを一般式で表すと、
![]()
となり、この式の意味は、aをx乗するとnになると読み取ることができます。ちなみに、各パラメータの呼び名は、aが底(てい)、nが真数、xが対数です(名称を覚える必要はありません)。
底が10の対数を常用対数といい、log102やlog103などは計算問題でよく使うため、数値を暗記している方もいるかもしれません。log102は、10を何乗したら2になるか…ということですが、正解は0.301となります。同様にlog103=0.477です。
ただし、電験三種の試験では、これらの情報(log102=0.301など)は問題文で与えられるため、暗記しなくて大丈夫です。
対数の計算は指数のときと同様にちょっと独特なので、その計算方法についてはしっかり身につけておかなければなりません。押さえておくべき計算式は、真数が積の形、商の形、累乗数の形の3パターンです。
以下にひとつずつ解説していきます。
真数が積の形
ある対数の真数が積の形で表される場合、以下のように2つの対数に分解して和の形で表すことができます。
![]()
たとえば、計算問題の解いた結果「log106」という数値を導いたとします。しかし、もし問題文に「log102=0.301、log103=0.477とする。」としか書いていないとしたら「log106」がわかりません。そのようなときに上記の式変換を使うことで、求める値を計算することができます。
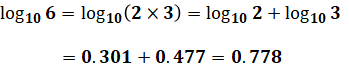
真数が商の形
対数の真数が掛け算で表されるときは、対数を分解して和の形に書き換えることができました。同様に、対数の真数が割り算で表されるときは、対数を分解して差の形に書き換えることができます。
![]()
この式の応用の仕方としては、「log105」の値を求めたいけれど、問題文では「log102=0.301とする。」としか与えられていない場合などです。この場合、次のように式変形することによって、log102の値をうまく利用して計算することができます。
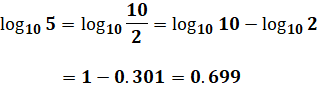
ちなみに、上式の計算過程で「log1010=1」としていますが、底の10を何乗したら真数の10になるかを考えると、10を1乗したら10になるので、この場合の対数は1です。このように、底と真数が同じ値の場合、対数は必ず1になります。
真数が累乗数の形
対数の真数が累乗数で表される場合、その累乗数の指数部分を対数の外に出すことができます。…というように文章で表現してもわかりにくいので、以下の式で確認してください。
![]()
この式の使いどころは、「log108」の値を求めたいけれど、問題文では「log102=0.301とする。」としか与えられていない場合などです。この場合、次のように式変形することによって、log102の値をうまく利用して計算することができます。
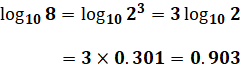
以上の3つの式変形のやり方さえ覚えれば、あとはそれらを組み合わせることで、複雑な対数を単純化することができます。

コメント