問 題
sinθ+cosθ=a(aは定数)のとき、sinθcosθ及びsinθ-cosθの組合せとして正しいのはどれか。
ただし0<θ<π/4とする。
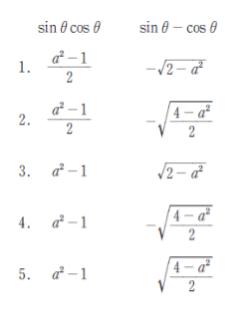
解 説
解法1【三角関数の知識を使う】
sinθ+cosθ = a の両辺を二乗します。
ここで、sin2θ+cos2θ = 1 です。
(sinθ+cosθ)2 = a2
sin2θ+2sinθcosθ + cos2θ = a2
1 + 2sinθcosθ = a2
∴ sinθcosθ = a2 -1 /2
です。正解は 1 or 2 です。
また、sinθ – cosθ を直接は求めることはできませんが、二乗すれば
(sinθ – cosθ)2
=sin2θ+cos2θ -2sinθcosθ
=1-2sinθcosθ
=1-2 ×(a2 – 1/2)
=1-(a2 -1)
=2-a2
なので±√ します。sin θ ー cos θ は0~π/4 で明らかに負なので、答えはー√ 2-a2 です。
以上より、正解は 1 です。
【解法2 具体的な数で考える】
θを、有名角である 30°とします。
sin30° = 1/2 = 0.5
cos30° = √3/2 です。
√3 ≒ 1.7 なのでcos30° ≒ 0.85 です。
従って、
a = sin30° + cos30°
≒ 0.5 + 0.85
≒ 1.35 です。
すると、a2 = (1.35)2 ≒ 1.8です。
a2 – 1 ≒ 0.8 とわかります。
(a2 – 1)/2 ≒ 0.4 です。
一方、
sin30°cos30°
= 1/2 × √3/2
≒ 0.5 × 0.85
≒ 0.4 です。
以上より、sin30°cos30° ≒ (a2 – 1)/2 です。
従って、正解は 1 or 2 です。
以下、選択肢 1,2 の検討をします。
θ = 30°の時、a2 ≒ 1.8 でした。よって、2-a2 ≒ 0.2 です。√0.2 は、大体 0.4~0.5 です。(√0.2 とは「二乗したら 0.2 になる数」です。0.42 = 0.16,0.52 = 0.25 なので、√0.2 は0.4~0.5 ぐらいとわかります。)
sin30°-cos30°
≒ 0.5 – 0.85
≒ -0.35
だいぶ近いです。
一方、4-a2 = 2.2 なので(4-a2)/2 ≒ 1.1 です。√をとってもほぼ 1 です。明らかに誤りです。
以上より、正解は 1 です。

コメント