問 題
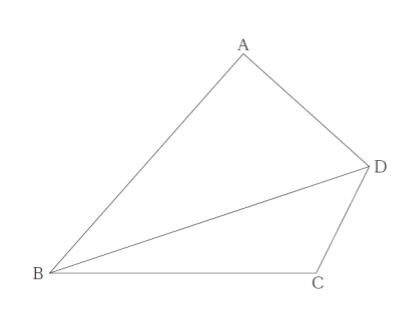
図のような三角形ABD と三角形BCD を合わせた四角形ABCD がある。AB =2√3,BC= √10 ,CD= √2 ,DA =2 ,∠BDA = 60°のとき,四角形 ABCD の面積はいくらか。
1. 4
2. 2√5
3. 3√3
4. 2+2√3
5. 3+2√2
解 説
三角形 ABD については、公務員試験頻出基本事項「1 : 2 : √3 の三角形」と判断できないといけません。A が 90° の直角三角形です。従って ABC の面積は 1/2 × 2 × 2√3 = 2√3 です。
三角形 BCD の面積については、以下のような解き方が考えられます。
【BCDの面積の求め方1】
三角形 ABD の辺の比が1:2:√3です。よって、BD の長さが 4 です。BDを底辺と考え、点C から垂線の足を降ろし、高さを求めようと考えます。 三平方の定理を使いやすくするために、x を以下のようにおきます。
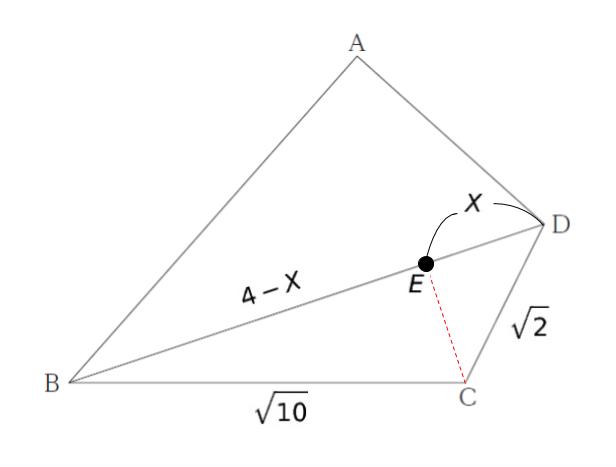
三平方の定理より、(4-x)2 + CE2 = 10、x2 + CE2 = 2 です。2つの式の辺辺引くと「-8x + 16 = 8」 です。よって、x = 1 とわかります。BDを底辺と見ることで三角形 BCD の面積は 1/2 × 4 × 1 = 2 です。従って、四角形 ABCD = ABD + BCD = 2√3 + 2 となります。
【BCDの面積の求め方2】
3辺わかっているため、余弦定理を用います。
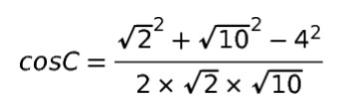
計算すると、cosC = -1/√5 です。よって、sinC = 2/√5 です。S = absinC/2 より (√2 × √ 10 × 2/√5) /2 = 2 です。従って、四角形 ABCD = ABD + BCD = 2√3 + 2 です。
以上より、正解は 4 です。

コメント