過去問 H30年 国家一般職（高卒 基礎）No.18解説

　問 題　　　　　

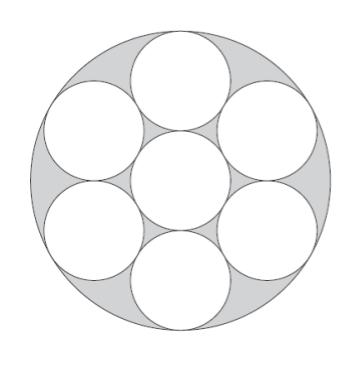
図のように，一つの小さな円の周りに，同じ大きさの円が六つ重ならないように接しており，さらに，その六つの円が一つの大きな円に接している。網掛けの部分の面積が 2 m² であることが分かっているとき，大きな円の面積はいくらか。

1． 6 m² 
2． 7 m² 
3． 8 m² 
4． 9 m² 
5． 10 m² 

 

 

 

 

 

　解 説　　　　　

円の面積は、半径 r の時、πr² です。

小さな円の半径を r とおきます。
図より、大きな円の半径は 3r です。大きな円の面積は π(3r)² = 9πr² と表せます。一方、小さな円１つの面積は πr² です。

図より
『大きな円の面積＝小さな円７つ＋網掛け部分』　です。従って、9πr² = 7πr² + 2 です。∴ πr² = 1 → 大きな円の面積は 9 です。

以上より、正解は 4 です。