問 題
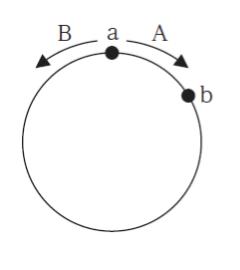
図のような円形のコースがあり,Aはa地点から時計回りに,Bはa地点から反時計回りに,それぞれ一定の速さで歩くこととした。まずBが先に出発し,その 2 分後にAが出発したところ,Aが出発して1 分後にb地点で, 2 人は初めてすれ違った。
Aは 30 m/分の速さで歩いており,b地点ですれ違った時点で,AはBが歩いた距離の 0.2 倍の距離を歩いたことが分かっているとき,次に 2 人がすれ違うのはb地点ですれ違ってから何分何秒後か。
1. 2 分 10 秒後
2. 2 分 15 秒後
3. 2 分 20 秒後
4. 2 分 25 秒後
5. 2 分 30 秒後
正解 (2)
解 説
A は 30m/分で歩いていたので、1 分間で A が移動した ab 間の距離は 30m です。この時「A は B が歩いた距離の 0.2 倍の距離を歩いた」ので、B は 30 ÷ 0.2 = 150m 歩いています。従って、円形のコース1周は、30 + 150 = 180m です。また、B は3分間で 150m 歩いているから、B の歩く速さは 50m/分 です。
b 地点ですれ違ってから、次に2人がすれ違うのは、2人の歩いた距離の合計が 180m になる時です。1 分間で、2人は合わせて 30 + 50 = 80m 歩きます。180 ÷ 80 = 2.25 分 です。※※ 0.25 分 = 15 秒です。選択肢 4 にとびついてはいけない問題!最後まで焦らずに!
以上より、正解は 2 です。

コメント