過去問 H30年 国家一般職（高卒 基礎）No.15解説

　問 題　　　　　

箱の中に赤玉が 3 個，白玉が 5 個，青玉が 2 個の合計 10 個の玉が入っている。この箱から同時に 3 個の玉を取り出したとき，それら 3 個の玉が全て同一の色にならない確率はいくらか。

 

 

 

 

 

 

　解 説　　　　　

確率とは、該当する通り/全ての通り　です。本問において、全ての通りは、玉 10 個から 3 個取り出した通りです。 ₁₀C₃ と表せます。

そして、該当する通りは、「全て赤」か「全て白」を　全ての通りから引くことで求めることができます。「全て赤」、「全て白」は それぞれ ₃C₃、₅C₃ 通りと表せます。

従って、求める確率は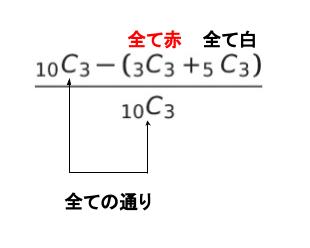

となります。

・₁₀C₃ = 10!/3!7! = 10×9×8/3×2×1 = 120
・₃C₃ = 1
・₅C₃ = 5!/3!2! = 5×4/2 = 10 です。

代入して計算すると、109/120 です。

以上より、正解は 5 です。