公務員試験 H30年 国家一般職(化学) No.19解説

　問 題　　　　　

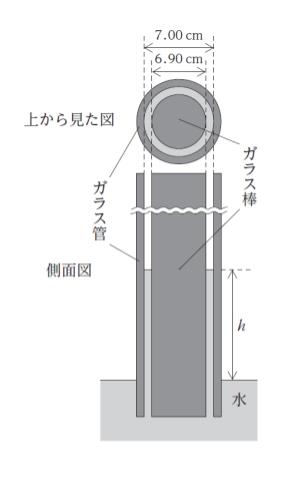
図のように、直径 6. 90 cm のガラス棒を、内径 7. 00 cm のガラス管の中に中心軸が一致するように入れたものを、水槽中に鉛直に立てると、毛管現象により環状の隙間を、水面からの高さ h 〔cm〕まで水が上昇した。このときの h はおよそいくらか。

ただし、重力加速度の大きさを 10 m・s^-2、水の表面張力 γ を7. 00 × 10^-2 N・m^-1、水の密度を 1. 00 × 10³ kg・m^-3、ガラスと水の接触角を 0° とする。なお、半径 r の球状の水滴における表面の内側と外側の圧力差は 2γ/r である。

1.  1. 4 cm
2.  2. 8 cm
3.  4. 2 cm
4.  5. 6 cm
5.  7. 0 cm

 

 

 

 

 

　解 説　　　　　

「吸い上げられている水の重さによる圧力」と、「表面張力による圧力差」が等しいと考えられます。片方の隙間に注目します。

まず、水による圧力 Pw を考えます。底面積を S とすれば、隙間で吸い上げられている水の体積 V = Sh です。その重さは V×（水の密度） = Sh × (1.00 × 10³ kg/m³) です。

下向きの力は 重力加速度 g をかければ , 1.00 は略すと Sh × (10⁴ kg/m²s²) です。これを底面積 S で割れば圧力です。

h は cm なので 「×10^-2 m」 として単位を m になおしておくと、Pw = h × 10² kg/m・s²・・・(1) です。この単位ですが、kg/ms² = kgm/m²s² = N/m²（∵N = kg・m/s²）です。

一方、表面張力による圧力差 Pγ は 2γ/r と書いてあります。r は 0.05cm です。単位を m になおしておくと 5 × 10^-4 m です。よって Pγ = 2 × 7.00 × 10^-2 / 5 × 10^-4 = 2.8 × 10² N/m²・・・(2) です。

(1) と (2) を比較すれば、h = 2.8 cm とわかります。

以上より、正解は 2 です。