問 題
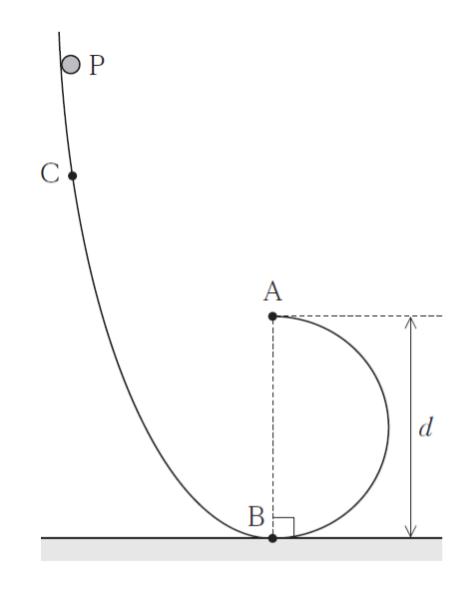
図のように,直径 d の半円筒面 AB を含む滑らかな曲面が,水平面に固定されている。曲面上の十分高い位置から小球 P を静かに放すと,小球 P は曲面を滑り落ちた後に半円筒面 AB で円軌道を描いて点 A から飛び出す。いま,小球 P が点 A から飛び出すような,最小の高さにある点 C から小球 P を静かに放した。このとき,点A における小球 P の速さとして最も妥当なのはどれか。ただし,重力加速度の大きさを g とする。
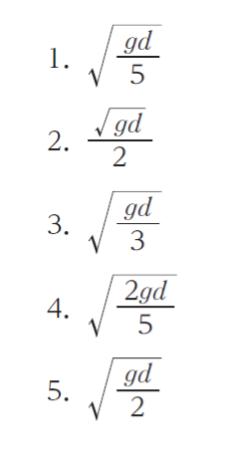
解 説
「円軌道を描いて飛び出す」ため、飛び出す瞬間まで円運動をしていなければいけない という点がポイントです。
なんとなく、高さ d からボールを転がせば、B 点で 位置エネルギーが全て運動エネルギーになり、また A 点で運動エネルギーが全て位置エネルギーになればよいような気がするのではないでしょうか。しかしそれでは A 点に到達して、v = 0 だから、後は真下に落っこちるだけです。滑り台のラストを思い出すとイメージしやすいのではないかと思うのですが、勢いのままシュッと飛び出すような速度が必要となります。
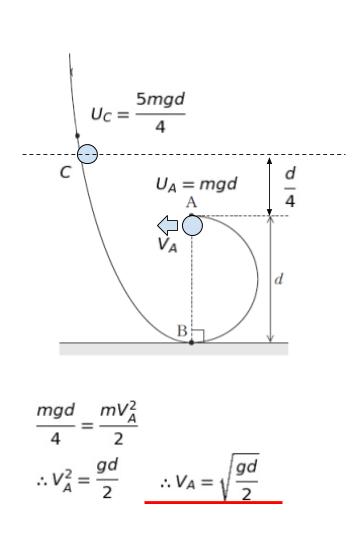
まず「小球 P が点 A から飛び出すような最小の高さ」について考えます。点A,B での速度を VA,VB とおけば、力学的エネルギー保存則より、m(VB)2/2 = mgd + m(VA)2/2 です。
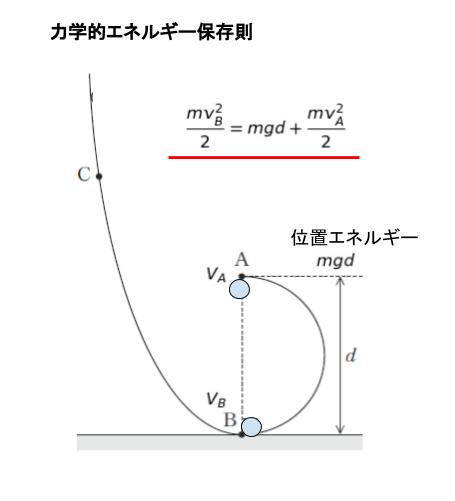
円運動をする場合「向心力」が働きます。向心力は質量と速さを用いて、mV2/(d/2) = 2mV2/d です。これは A 点においては『垂直抗力+重力』です。A 点における垂直抗力を NA とおけば、NA + mg です。よって、2m(VA)2/d = NA + mg です。円運動するとは、NA≧0 と解釈することができます。
以上より、 VB ≧√5g(d/2) を導くことができます。 (この問題は d/2 = r として、「√5gr」 が、このパターンの最低限必要な速度ということを「基礎知識」として知っている前提の問題である気もします。余裕があればぜひ知識としておさえておきましょう!)
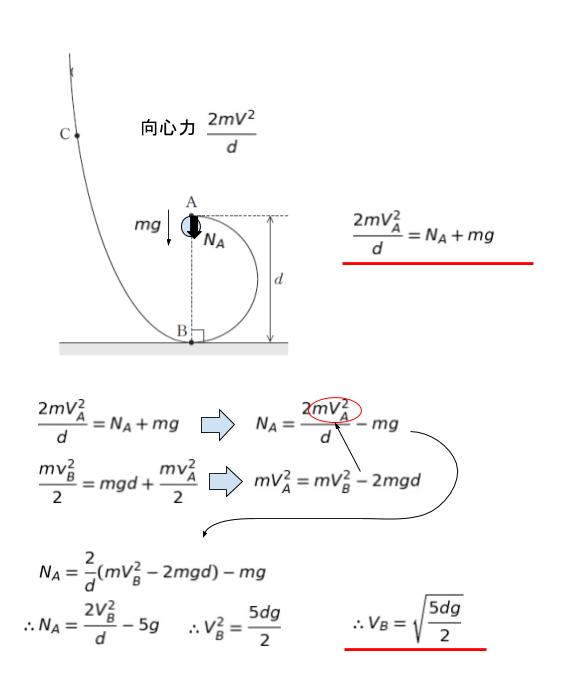
従って、最小値は VB = √5g(d/2) です。つまり、VB2 = 5gd/2 です。従って、B 地点で 5mgd/4 の運動エネルギーを有します。この運動エネルギーを有するような最小の高さは 「5d/4」 です。
高さ 5d/4 からボールを離し、一回転して点 A にいる時、位置エネルギーが UA = mgd なので、mgd/4 = mVA2/2 が成立します。∴VA2 = gd/2 ∴VA = √gd/2 です。
以上より、正解は 5 です。

コメント