問 題
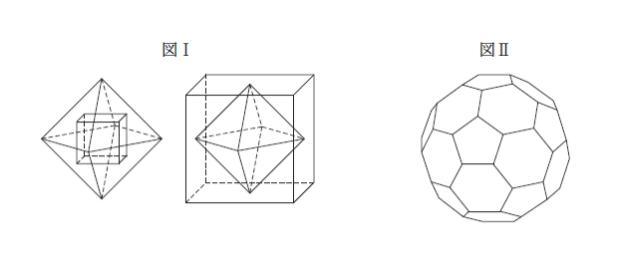
図Ⅰに示すように,正八面体と立方体は,正八面体の隣り合う面(一辺で接する面)の中心を結んでできる立体は立方体に,また,立方体の隣り合う面の中心を結んでできる立体は正八面体になるという関係にある。
このとき,図Ⅱのような切頂二十面体(いわゆるサッカーボール型の立体)の隣り合う面の中心を結んでできる立体として最も妥当なのはどれか。
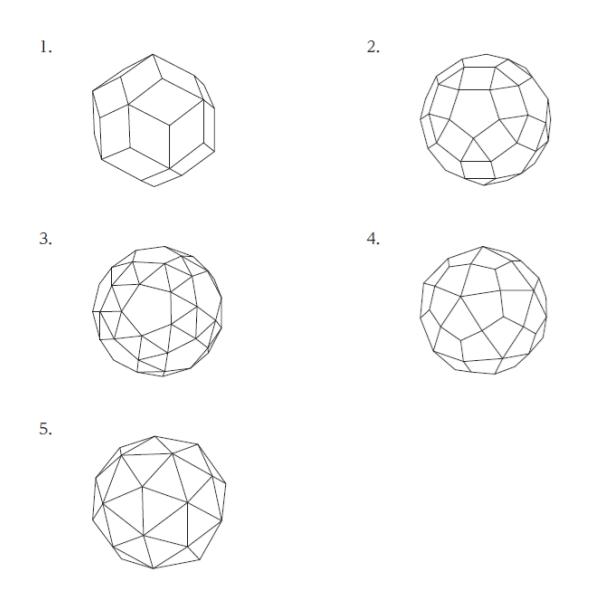
正解 (5)
解 説
幾何に詳しい人にとっては知識ですが、公務員試験としては「具体的に考える」タイプの問題と考えられます。図Ⅱの面の中心をいくつか結ぶと面としては「正三角形」ができそうと判断できるのではないでしょうか。
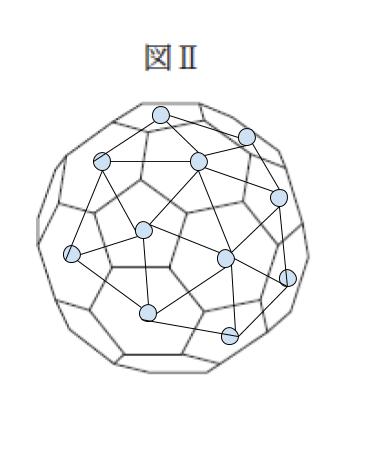
また、図Ⅱの立体が切頂二十面体とあるので、面の中心は 20 個あると考えられます。20 個の点が、新たな立体の頂点となる、ということです。「正三角形、頂点 20 個」から正二十面体と判断できるのではないかと思われます。
もしくは選択肢を1つ1つ検討すれば、選択肢 1 ~ 4 は四角形や五角形が含まれる点から誤りと判断できると考えられます。
以上より、正解は 5 です。

コメント