問 題
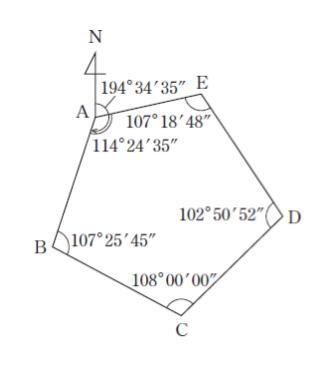
図のような地点A~E に対して,閉合トラバース測量を行った。図のように,測線AB の方位角と各地点の内角がそれぞれ分かっているとき,測線CD の方位角はおよそいくらか。
1. 30° 09′ 40 m
2. 50° 00′ 20 m
3. 54° 00′ 00 m
4. 209° 50′ 20 m
5. 329° 50′ 20 m
正解 (2)
解 説
トラバースとは
ある地域を測量する場合の骨組の一種です。測量に必要な測点を定め、順次、測線を結んで折れ線となったものをいいます。トラバースの各測点の位置を求める測量をトラバース測量といいます。
測線 AB の方位角として 194°34’35’’ が与えられているように、始点から真北に線を引き、その線と測線のなす角が方位角です。点 C から真北に補助線を引き、AE との交点を F とおきます。
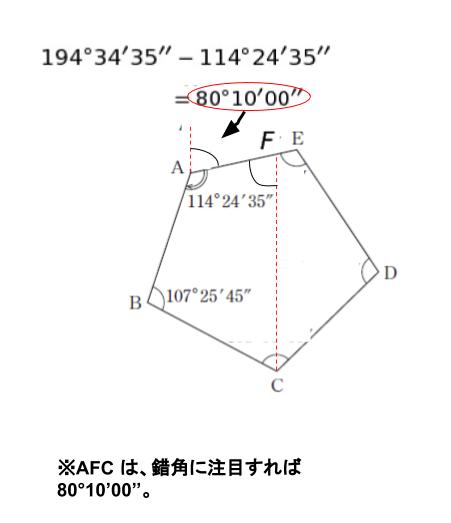
□ ABCF に注目すれば、∠BCF は 57° 59’ 40’’ とわかります。
(∵ 360 – (114°24’35’’ + 107°25’45’’ + 80°10’00’’)= 57° 59’ 40’’
※分、秒については 60 で桁が繰り上がる点に注意が必要です。)
∠C は 108°00’00’’ なので、求めたい方位角である ∠ FCD は 108° ー 57° 59’ 40’’ です。選択肢を参考にすれば計算しなくてもわかります。 50°00’20’’ です。
以上より、正解は 2 です。

コメント