問 題
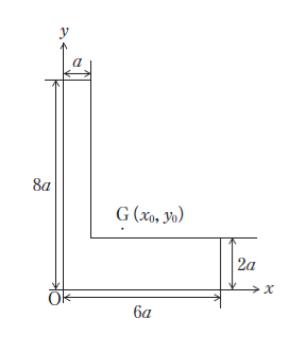
図のような断面における図心 G の座標(x0、y0)の組合せとして最も妥当なのはどれか。

正解 (2)
解 説
長方形の図心は対角線の交点です。これは基礎知識です。
複雑な図形は単純な図形に分けて考えます。本問では、2つの長方形に分けて考えます。それぞれの長方形の図心は (a/2,5a)、(3a,a) です。
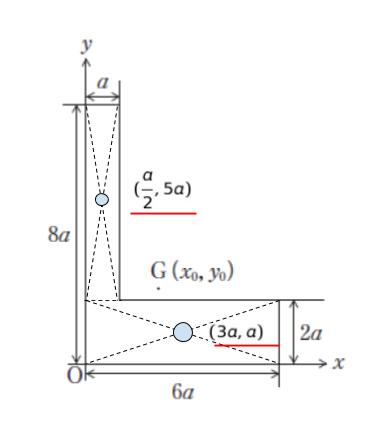
2つの図心に長方形の質量を1点にあつめた質点2つを考えます。それぞれの質量は面積比になると考えられます。従って、 6a2 : 12a2 = 1 : 2 の重さの比となります。2つの質点に対する釣合の点を考えることで全体の図心を求めることができます。
きちんと計算して求めてもよいのですが、明らかに G の x0 は 3a よりも小さいとわかります。これにより正解は 1 or 2 に絞られます。
y 座標のみに注目します。
5a と a の距離は 4a です。
2:1に内分する点を考えれば y 座標は a + 4a/3 = 7a/3 です。
以上より、正解は 2 です。

コメント