問 題
テーブルの上にコインが 6 枚あり、 3 枚が表向き、 3 枚が裏向きに置かれている。
この 6 枚のコインをそれぞれ 3 枚ずつの二つのグループにランダムに分け、一方のグループのコインを全てひっくり返す(表向きのコインは裏向きに、裏向きのコインは表向きにする)。
このとき、表向きになっているコインの枚数が二つのグループで等しい確率はいくらか。
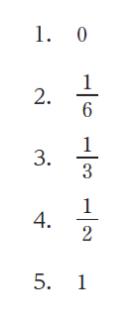
正解 (5)
解 説
具体的に考えます。
3枚ずつのグループに分けた時に、片方のグループが
1:表3枚→もう片方のグループは裏3枚
2:表2枚裏1枚→もう片方のグループは表1枚裏2枚
3:表1枚裏2枚→もう片方のグループは表2枚裏1枚
4:裏3枚→もう片方のグループは表3枚
という4パターンが考えられます。
すると、どのパターンも、一方のグループのコインを全てひっくり返せば、他方のグループの表のコインの枚数と等しくなります(!)。従って、求める確率は 1 です。
以上より、正解は 5 です。
類題 H28no9

コメント