問 題
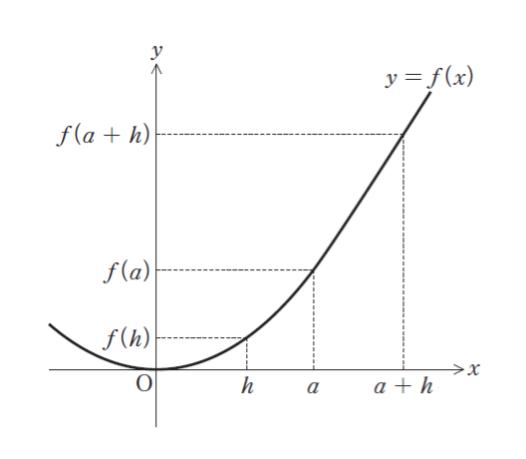
図のような関数 y = f(x) の x = a における微分係数 f’(a) として正しいのはどれか。ただし、f(x) は x = a で微分可能であるものとする。
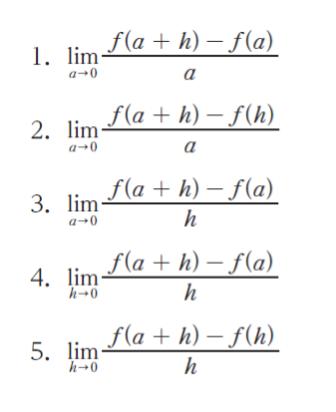
正解 (4)
解 説
「x = a における微分係数 f’(a)」というのは「3」のような数値です。その数値がグラフにおいて何を意味するかというと「x = a における グラフの接線の傾き」です。これは基礎知識です。
a と a+h の幅 h が限りなく0に近づく時、「f(a+h)-f(a)/h」(「2点を結ぶ線分の傾き」が、x = a におけるグラフ の接線の傾きに限りなく近づきます。問題文のグラフと照らし合わせて、ぜひ納得感を持ってもらえればと思います。従って、「h → 0」 となっているものが正解です。正解は 4 or 5 です。
選択肢 5 ですが
h → 0 の時に「f(a)/0」 に近づいていきます。f(a) は「3」のような具体的数値なので「3/0」に近づきます。つまり、とんでもなく大きな値となるため、x = a におけるグラフの接線の傾きには近づいていきません。よって、選択肢 5 は誤りです。
以上より、正解は 4 です。

コメント