公務員試験 H30年 国家一般職(土木) No.14解説

　問 題　　　　　

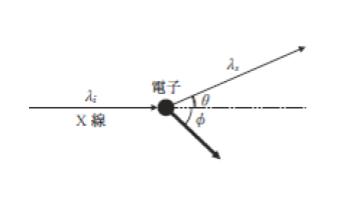
図のように，真空中で静止している電子に向けて波長 λi の X 線を入射させたところ，その入射方向に対して角度 θ の方向に波長 λs の X 線が散乱され，電子は角度 Φ の方向に跳ね飛ばされた。

プランク定数を h とするとき，跳ね飛ばされた電子の運動量の大きさとして最も妥当なのはどれか。

なお，波長 λ の X 線の運動量の大きさ p は p = h/λ と表せる。

 

 

 

 

 

　解 説　　　　　

衝突前後の運動量が保存される点に注目します。真横方向と、真縦方向に分けて考えます。また、電子の質量を m とおけば、求めたい電子の運動量は P とおきます。

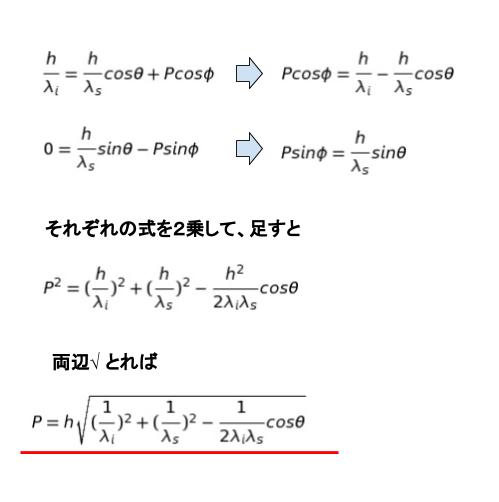
横方向について、衝突前後で h/λi = h/λs cosθ + PcosΦ・・・（１） が成り立ちます。また、縦方向について h/λs sin θ = PsinΦ・・・（２） が成り立ちます。

求めたいのが P なので、（１）の右辺を Pcos Φのみにした上で、それぞれの式を２乗して足せば、√の中身は「ー」、「cosθ」となっているものが正解とわかります。

以上より、正解は 1 です。