問 題
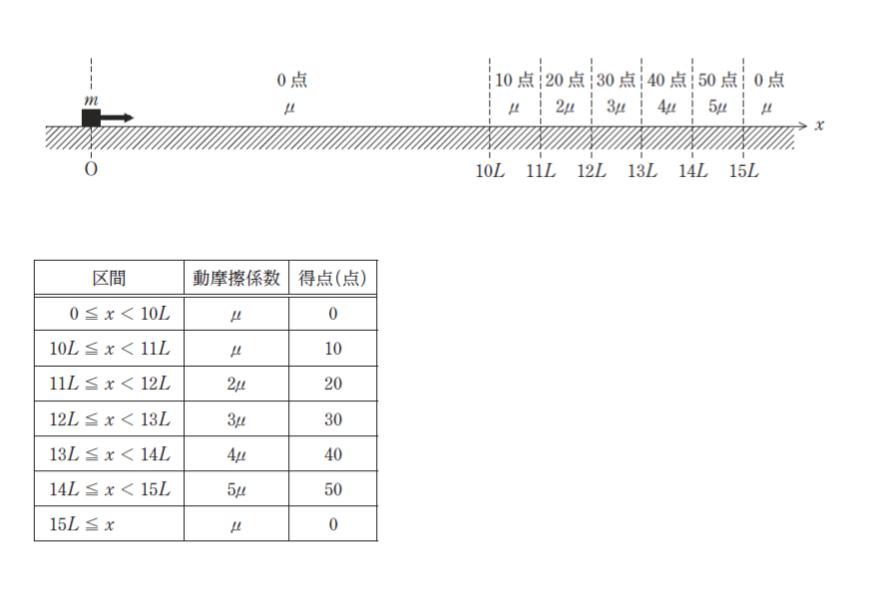
図のように、原点O に置かれた質量 m の小物体に x 軸正方向の撃力を加えて粗い水平面上を滑らせ、小物体が静止した区間に対応する得点を獲得するゲームがある。
このゲームを3回行い、いずれも異なる得点を獲得した上で、得点の合計を 100 点にしたい。
3 回のゲームを通じて、撃力によって小物体に与えるエネルギーの合計を W とするとき、W の最小値として最も妥当なのはどれか。
ただし、各区間における小物体と水平面の間の動摩擦係数及び得点はそれぞれ表のとおりとする。また、重力加速度の大きさを g とする。
1. 42μmgL
2. 44μmgL
3. 46μmgL
4. 48μmgL
5. 50μmgL
正解 (2)
解 説
動いている物体は動摩擦力を受けます。F動摩擦力= μ’N です。μ’ が動摩擦係数です。質量 m なので、下向きに mg の力が働きます。垂直抗力も mg です。動摩擦係数が μ の区間において、小物体は mgμ の摩擦力を受け続けます。
『摩擦により失われたエネルギー = 仕事』 が成立します。『仕事=力×距離』です。例えば 10μmgL のエネルギーを与えると、ちょうど 10L の所まで小物体は移動します。 10L≦x<11L であれば 10 点なので、10 点です。
合計 100 点で、「3回いずれも異なる得点」であることに注意すれば、20,30,50 点を取る時、W は最小と考えられます。つまり、11L,12L,14L まで小物体を移動させればよいです。それぞれ 11μmgL、13μmgL、20μmgL のエネルギーが最低でも必要です。合計すれば 44 μmgL となります。
以上より、正解は 2 です。

コメント