問 題
一定の速さ v で等速直線運動している質量 m の小球に撃力を加えたところ、小球は、はじめの進行方向から角 2θ だけ傾いた方向に速さ v で進んだ。
このとき、小球に与えた力積の大きさとして最も妥当なのはどれか。
ただし、重力の影響は無視するものとする。
1. mv|sinθ|
2. 2mv|sinθ|
3. 2mvsin2θ
4. 2mv|cosθ|
5. 2mv(1 – cosθ)
正解 (2)
解 説
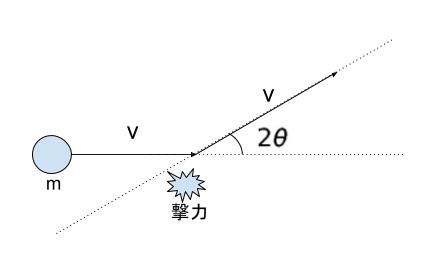
力積は、「力 × 力がかかっている時間」 です。力積は運動量の変化に等しいという点がポイントです。
運動量=質量 × 速さ です。
運動量を x 軸方向、y 軸方向に分けて考えます。撃力を受ける前は、それぞれの運動量を Px,Py とすれば、Px = mv、Py = 0 です。撃力を受けた後は 2θ傾いているから、Px = mvcos2θ、Py = mvsin2θ です。
従って、運動量の変化に注目すれば、ΔPx = mv – mvcos 2θ、ΔPy = -mvsin 2θ です。
運動量の変化の大きさ |ΔP|=√(ΔPx)2 + (ΔPy)2 です。以下のように計算できます。

以上より、正解は 2 です。

コメント