問 題
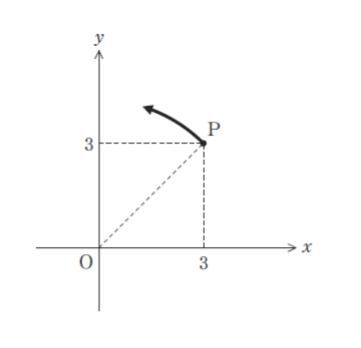
xy 平面上において,点P(3、3)を,原点O を中心として図の矢印の向きに60°回転させた点の x 座標の値はいくらか。
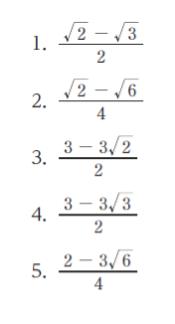
正解 (4)
解 説
回転移動は「複素平面で考えて cos θ + isinθ をかける」か、「回転行列」をかけるかで、移動先を求めます。
【複素平面で回転】
A = 3+3i を考えます。 60°回転した先を A’ とすれば、A’ = (cos60°+ isin60°)(3+3i) = (1/2 + √3i/2)(3+3i) = 3/2 – 3√3/2 + (3/2 + 3√3/2)i です。
従って、x 座標は (3-3√3)/2 です。正解は 4 です。
【回転行列で回転】
cos60°=1/2、sin60°=√3/2 なので、回転行列は以下のようになります。
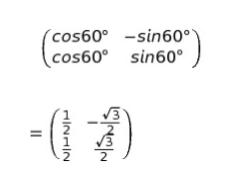
(3,3) に回転行列を作用させる、つまり積を計算すれば、以下のようになります。
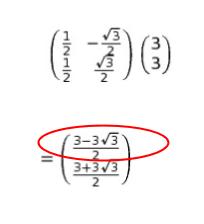
以上より、正解は 4 です。

コメント